Электропроводность. Закон Ома.
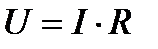 – закон Ома.
– закон Ома.
Выпишем это уравнение в дифференциальной форме с помощью уравнения (2.1):
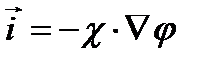 ,- закон Ома ,- закон Ома
| (2.5) |
Где 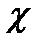 - удельная электропроводность,
- удельная электропроводность, 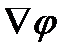 - электрический потенциал.
- электрический потенциал.
В одномерном виде:
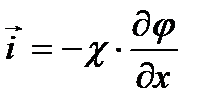
| (2.6) |
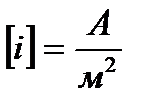 - плотность тока
- плотность тока
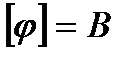
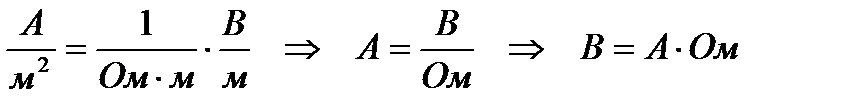
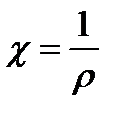 ,
, 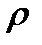 - предельное сопротивление системы.
- предельное сопротивление системы.
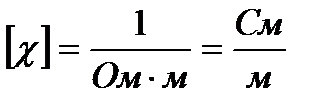 - удельная электропроводность среды.
- удельная электропроводность среды.
Уравнения (2.5), (2.6) – закон Ома в дифференциальной форме:
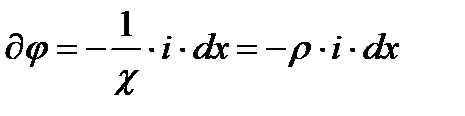 , ,
| (2.7) |
это прилагается к некоторому слою толщиной dx.
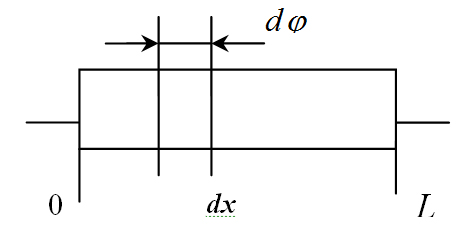
Продифференцируем уравнение (2.7): 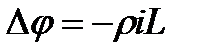
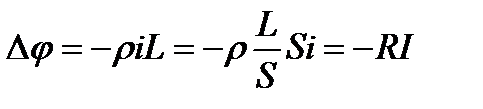 , здесь S – сечение, а
, здесь S – сечение, а 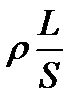 - сопротивление.
- сопротивление.
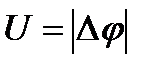 , тогда
, тогда 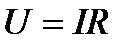 - закон Ома в интегральной форме.
- закон Ома в интегральной форме.
Минусы в уравнениях (2.5), (2.6)?
В этом случае электрический потенциал меняется слева направо.
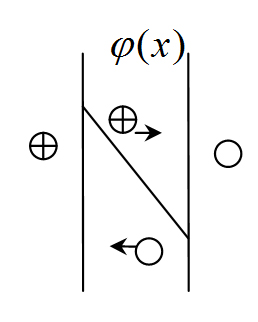
Здесь движение положительно заряженных частиц вдоль оси Ох.
За положительное направление тока принимается то направление, в котором движутся положительно заряженные частицы.
Для положительно заряженных частиц: 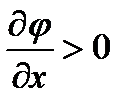 , i>0.
, i>0.
Для отрицательно заряженных частиц: 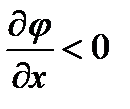 - отсюда и появляется знак минус в дифференциальной форме.
- отсюда и появляется знак минус в дифференциальной форме.
Пусть 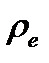 - плотность электрического заряда, тогда
- плотность электрического заряда, тогда
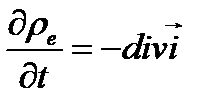
Подставив это уравнение в уравнение (2.5), получим:
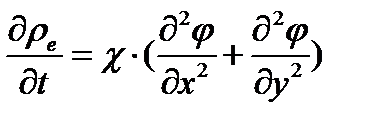
В частном случае, если 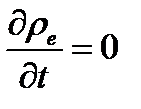 , то:
, то:
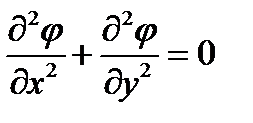 - закон Лапласа.
- закон Лапласа.
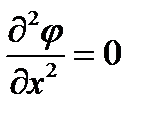 - закон Лапласа в одномерном случае. Отсюда:
- закон Лапласа в одномерном случае. Отсюда:
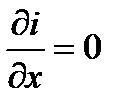 , то есть плотность тока не меняется по координате.
, то есть плотность тока не меняется по координате.
Дата добавления: 2015-10-21; просмотров: 803;
