Определение параметров теоретического закона распределения методом вероятностной бумаги
Достоинство метода вероятностной бумаги – возможность обработки всех видов информации: полной, усеченной и многократно усеченной.
Кривая накопленных опытных вероятностей или интегральная кривая теоретического закона распределения носит, естественно, криволинейный характер. По внешнему виду этой кривой трудно определить, какому закону подчиняется рассеивание показателя надежности, и невозможно определить параметры этого закона. Кроме того, в случае усеченной информации и известного закона распределения на такой график удается нанести только начальные точки информации.
Функциональную сетку вероятностной бумаги составляют так, чтобы нанесенная на эту бумагу интегральная функция распределения была представлена прямой линией (интегральная прямая). Для выпрямления интегральной функции на ось ординат вероятностной бумаги наносят отметки значений F(T) (0,01; 0,05; 0,10; 0,20 и т.д. до 0,95). При этом расстояние отметок от начала координат делают равными значениям квантилей отмеченных величин. Значения нормированных (по параметру s для ЗНР и по параметру a для ЗРВ) квантилей приведены в таблицах Б7 и Б8 приложения Б. Квантилем называется нормированное значение показателя надежности, соответствующее данной величине интегральной функции F(T) или накопленной опытной вероятности åРi.
Затем на функциональную сетку вероятностной бумаги наносят все или выбранные (i-е) точки исходной информации в соответствии с их координатами: абсциссой (величина показателя надежности Тдрi ) и ординатой (величина накопленной опытной вероятности 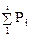 ).
).
Дата добавления: 2015-10-19; просмотров: 1261;
