Значения накопленных опытных вероятностей (частостей). Значения накопленных вероятностей (последняя строка ряда) определяют суммированием вероятностей по интервалам.

Значения накопленных вероятностей (последняя строка ряда) определяют суммированием вероятностей по интервалам.

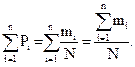(5)

Для нашего примера:

;

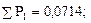
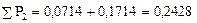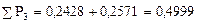
и т.д. по другим интервалам.

2.1.3 Определение числовых характеристик

Основными числовыми характеристиками распределения случайной величины являются среднее значение, среднее квадратическое отклонение и коэффициент вариации.

Среднее квадратическое отклонение представляет собой абсолютную меру, а коэффициент вариации – относительную меру рассеивания (разброса) случайной величины. При объеме выборки (информации) N³25 их определяют следующим образом.

Среднее значение ресурса определяется по формуле:

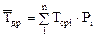, мото-ч., (6)

где Т_срi – значение ресурса в середине i-го интервала;

Р_i – опытная вероятность в i-ом интервале.

Для нашего примера:

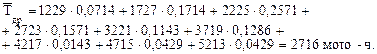
Среднее квадратическое отклонение определяется по формуле:

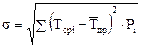,мото-ч. (7)

Для нашего примера:

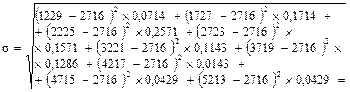
= 1009 мото-ч.

Коэффициент вариации определяется по формуле:

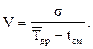(8)

Для нашего примера:

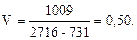
2.1.4 Проверка информации на наличие выпадающих точек

Проверку информации на наличие выпадающих точек осуществляют по формуле:

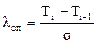, (9)

где T_i и T_i-1 – смежные точки в сводной ведомости информации (см. таблицу 1).

В нашем примере:

для наименьшего значения ресурса

Т₁=980 мото-ч.; Т₂=1272 мото-ч.; ;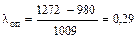

для наибольшего значения ресурса

Т₇₀=5460 мото-ч.; Т₆₉=5220 мото-ч.; ;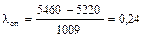

Полученные значения сравнивают с табличными значениями критерия Ирвина (Приложение Б, таблица Б1).

Если λ_оп < λ_т то информация достоверна, если же λ_оп > λ_т, то такие точки «выпадают», т.е. должны быть исключены из информации как недостоверные. В этом случае необходимо перестроить статистический ряд с учетом уменьшения количества информации за счет выпавших точек и вновь рассчитать 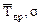и V.

В нашем случае при N=70 и доверительной вероятности a=0,95 табличное значение критерия Ирвина l_Т = 1,1, т.е. больше l_оп. Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.