Упражнения для самостоятельной работы. 1. Вычислите степени числа i:
1. Вычислите степени числа i:
1) 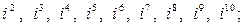
2) 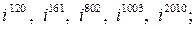
3) 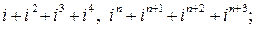
4) 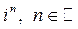 .
.
2. Выполните действия над комплексными числами в алгебраической форме:
1) 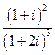 ; 2)
; 2) 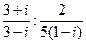 ; 3)
; 3)  ;
;
4) 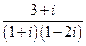 ; 5)
; 5) 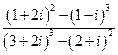 ; 6)
; 6) 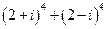 .
.
3.1) Даны два комплексных числа 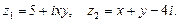 Определите, при каких действительных значениях х и y числа
Определите, при каких действительных значениях х и y числа 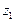 и
и 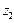 будут комплексно сопряженными.
будут комплексно сопряженными.
2) Найдите множество комплексных чисел, каждое из которых равно квадрату сопряженного с ним числа.
4. Запишите каждое из следующих комплексных чисел в тригонометрической и в показательной формах:
1) 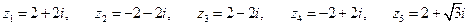 ,
,
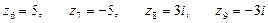 ;
;
2) 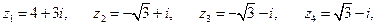
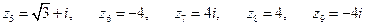 .
.
5. Выполните действия над комплексными числами в тригонометрической или в показательной формах; ответ запишите в алгебраической форме:
1) 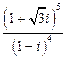 ; 2)
; 2) 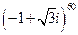 ; 3)
; 3)  ;
;
4) 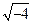 ; 5)
; 5) 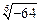 ; 6)
; 6) 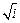 ;
;
7); 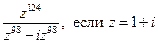 ; 8)
; 8) 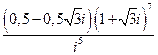 ; 9)
; 9) 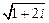 .
.
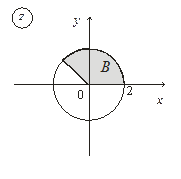
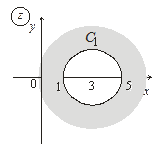
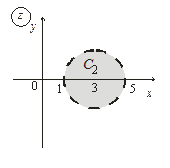
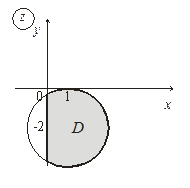
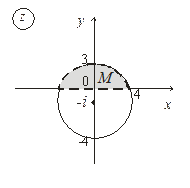
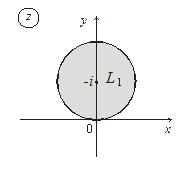
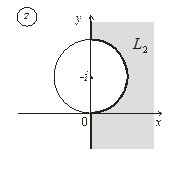
6. Постройте множества точек на комплексной плоскости:
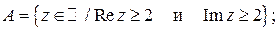
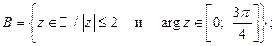
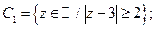
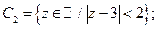
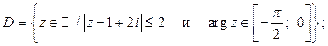
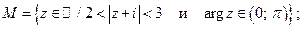
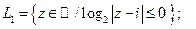
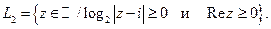
7. 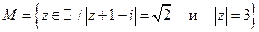 . Докажите, что
. Докажите, что 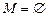 .
.
8. Найдите следующие множества:
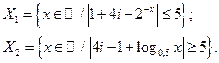
Ответы к упражнениям для самостоятельной работы
1. 1) 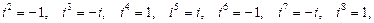
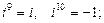
2) 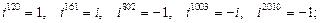
3) 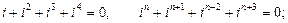
4) 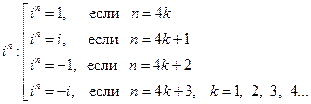
2. 1)  ; 2)
; 2) 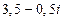 ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 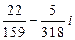 ; 6)
; 6) 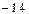 .
.
3. 1)  2)
2) 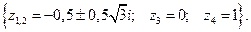
4. 1)  ;
;
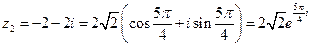 ;
;
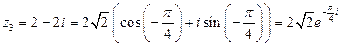 ;
;
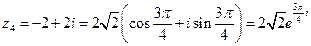 ;
;
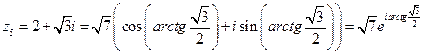 ;
;
 ;
;  ;
;
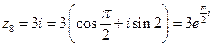 ;
; 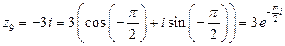 ;
;
2)  ;
;
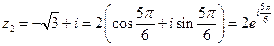 ;
;
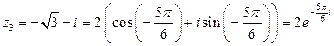 ;
;
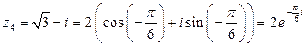 ;
;
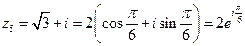 ;
; 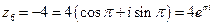 ;
;
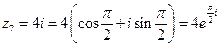 ;
; 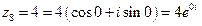 ;
;
 .
.
5. 1) 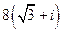 ; 2)
; 2)  ; 3)
; 3) 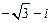 ; 4)
; 4) 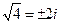 ;
;
5) 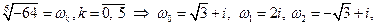

6) 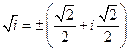 ; 7)
; 7) 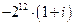 ; 8)
; 8) 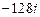 ;
;
9) 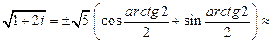
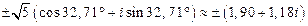 .
.
| 6. | 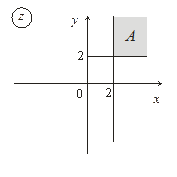
| 
|
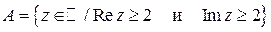
| 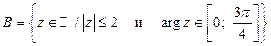
| |
| 
| |
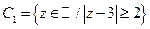
| 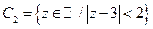
| |
| 
| |
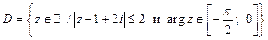
| 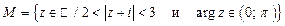
| |
| 
| |
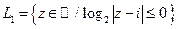
| 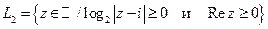
|
| 7. |  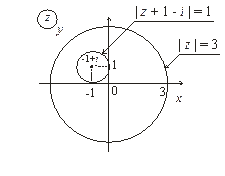
|
8. 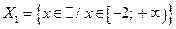 ;
; 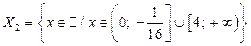 .
.
Вопросы для самопроверки
Что называется основными преобразованиями графика?
Что называется комплексным числом z?
Что такое мнимая единица?
Что такое действительная часть комплексного числа z?
Что такое мнимая часть комплексного числа z?
Что такое комплексно сопряженное число числу z?
Что такое противоположное число числу z?
Что такое комплексный ноль?
Что такое множество комплексных чисел?
Что такое чисто мнимое число?
Что такое равенство двух комплексных чисел?
Что такое равенство комплексного числа нулю?
Что называется разделением действительных и мнимых частей в комплексном равенстве?
Что называется действительной осью?
Что называется мнимой осью?
Что называется модулем комплексного числа?
Что такое аргумент комплексного числа z?
Что называется главным значением аргумента?
Что называется алгебраической формой комплексного числа z?
Что называется тригонометрической формой комплексного числа z?
Что такое сложение (вычитание) комплексных чисел?
Что такое основные свойства сложения комплексных чисел?
Что такое умножение комплексных чисел в алгебраической форме?
Что такое умножение комплексных чисел тригонометрической форме?
Что такое основные свойства умножения комплексных чисел?
Что такое деление комплексных чисел?
Что такое возведение комплексного числа в натуральную степень?
Что такое формула Муавра?
Что называется корнем степени n из комплексного числа z?
Сформулируйте теорему о значениях корня из комплексного числа
Что называется показательной формой комплексного числа?
Что называется действия над комплексными числами в показательной форме?
Что такое формулы Эйлера?
Глоссарий
алгебраической формой комплексного числа z называется…(стр. 149)
аргумент комплексного числа z это…(стр. 148)
возведение комплексного числа в натуральную степень 153 это…(стр. 153)
главным значением аргумента называется…(стр. 149)
действительная часть комплексного числа z это…(стр. 146)
действительной осью называется…(стр. 148)
действия над комплексными числами в показательной форме это…(стр. 155)
деление комплексных чисел это…(стр. 152)
комплексно сопряженное число числу z это…(стр. 146)
комплексный ноль это…(стр. 146)
комплексным числом z называется…(стр. 146)
корнем степени n из комплексного числа z называется…(стр. 153)
мнимая единица 146 это…(стр. 146)
мнимая часть комплексного числа z 146 это…(стр. 146)
мнимой осью 148 называется…(стр. 148)
множество комплексных чисел это…(стр. 147)
модулем комплексного числа называется…(стр. 148)
основные свойства сложения комплексных чисел это…(стр. 151)
основные свойства умножения комплексных чисел это…(стр. 152)
показательной формой комплексного числа называется…(стр. 155)
противоположное число числу z это…(стр. 146)
равенство двух комплексных чисел это…(стр. 147)
равенство комплексного числа нулю это…(стр. 147)
разделением действительных и мнимых частей в комплексном равенстве называется…(стр. 147)
сложение (вычитание) комплексных чисел это…(стр. 150)
тригонометрической формой комплексного числа z называется…(стр. 149)
умножение комплексных чисел в алгебраической форме это…(стр. 151)
умножение комплексных чисел тригонометрической форме это…(стр. 151)
формула Муавра это…(стр. 153)
формулы Эйлера это…(стр. 156)
чисто мнимое число 147 это…(стр. 147)
Дата добавления: 2015-10-19; просмотров: 1790;
