Основные свойства целых многочленов
| Свойство 1 (о тождественном равенстве алгебраических многочленов) |
Два алгебраических многочлена одной степени 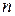 тождественно равны друг другу тогда и только тогда, когда совпадают их коэффициенты при одинаковых степенях переменной тождественно равны друг другу тогда и только тогда, когда совпадают их коэффициенты при одинаковых степенях переменной 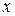 , то есть , то есть
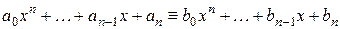 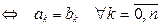 (3) (3)
|
w Тождество (3) справедливо при "x Î 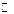 (или "x Î
(или "x Î 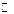 ), следовательно,
), следовательно,
оно справедливо при 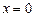 ; подставляя
; подставляя 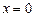 , получим аn = bn.
, получим аn = bn.
Взаимно уничтожим в (3) слагаемые аn и bn и поделим обе части на x:
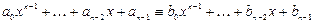 . (3')
. (3')
Это тождество тоже верно при "x, в том числе при x = 0, поэтому полагая x = 0, получим аn – 1 = bn – 1.
Взаимно уничтожим в (3') слагаемые аn – 1 и bn – 1 и поделим обе части на x, в результате получим
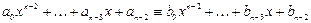 .
.
Аналогично продолжая рассуждение, получим, что аn – 2 = bn –2, …, а0 = b0.
Таким образом, доказано, что из тождественного равенства двух целых многочленов следует совпадение их коэффициентов при одинаковых степенях x.
Обратное утверждение справедливо очевидно, то есть если два многочлена имеют одинаковыми все коэффициенты, то они есть одинаковые функции, определенные на множестве 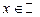 , следовательно, их значения совпадают при всех значениях аргумента
, следовательно, их значения совпадают при всех значениях аргумента 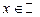 , что и означает их тождественное равенство. Свойство 1 доказано полностью. v
, что и означает их тождественное равенство. Свойство 1 доказано полностью. v
Пример (тождественное равенство многочленов)
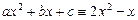
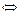
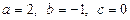 .
.
| Свойство 2 (о делении целого многочлена на разность (x – х0)) |
При делении многочлена 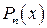 на разность на разность 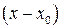 получается остаток, равный получается остаток, равный 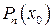 – значению этого многочлена в точке – значению этого многочлена в точке 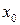 , то есть верно равенство , то есть верно равенство
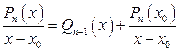 Теорема Безу (4)
где Теорема Безу (4)
где 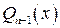 — целая часть от деления, является многочл. степени — целая часть от деления, является многочл. степени  . .
|
w Запишем формулу деления с остатком: Pn(x) = (x – х0)∙Qn – 1(x) + A,
где Qn – 1(x) — многочлен степени (n – 1),
A — остаток, который является числом вследствие известного алгоритма деления
многочлена на двучлен «в столбик».
Это равенство верно при "x, в том числе при x = х0; полагая 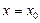 , получим
, получим
Pn(x0) = (x0 – x0)×Qn – 1(x0) + A Þ A = Pn(х0). v
Следствием доказанного свойства является утверждение о делении без остатка многочлена на двучлен, известное как теорема Безу.
| Теорема Безу (о делении целого многочлена на двучлен без остатка) |
Если число 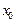 является нулем многочлена является нулем многочлена 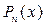 , то этот многочлен делится без остатка на разность , то этот многочлен делится без остатка на разность 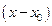 , то есть верно равенство , то есть верно равенство
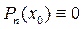 Þ Þ 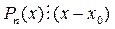 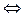 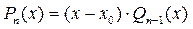 (5) (5)
|
w Доказательство теоремы Безу можно провести без использования ранее доказанного свойства о делении целого многочлена  на двучлен
на двучлен 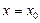 . Действительно, запишем формулу деления многочлена
. Действительно, запишем формулу деления многочлена  на двучлен
на двучлен 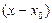 с остатком А=0:
с остатком А=0:
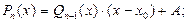
Теперь учтем, что 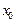 - это нуль многочлена
- это нуль многочлена  , и запишем последнее равенство при
, и запишем последнее равенство при 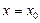 :
:
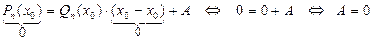 .v
.v
Примеры (разложение многочлена на множители с использованием т. Безу)
1) 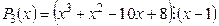 , так как P3(1) º 0
, так как P3(1) º 0
Þ 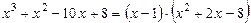 ;
;
2) 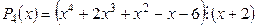 , так как P4(–2) º 0
, так как P4(–2) º 0
Þ  ;
;
3) 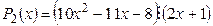 , так как P2(–1/2) º 0 Þ
, так как P2(–1/2) º 0 Þ 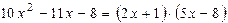 .
.
| Свойство 3 (о существовании нуля многочлена, основная теорема алгебры) |
Всякий алгебраический многочлен  степени n ³ 1 имеет, по крайней мере, один нуль, действительный или комплексный степени n ³ 1 имеет, по крайней мере, один нуль, действительный или комплексный
|
Доказательство этой теоремы выходит за рамки нашего курса. Поэтому примем теорему без доказательства.
Поработаем по этой теореме и по теореме Безу с многочленом Pn(x):
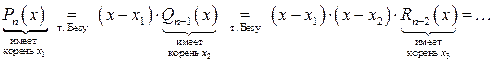 ;
;
после n-кратного применения этих теорем получим, что
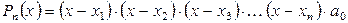 ,
,
где a0 — это коэффициент при xn в записи многочлена Pn(x).
| Свойство 4 (о разложении многочлена на линейные множители) |
Любой алгебраический многочлен степени  на множестве комплексных чисел разлагается на n линейных сомножителей, то есть верно равенство на множестве комплексных чисел разлагается на n линейных сомножителей, то есть верно равенство
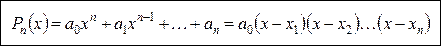 Разложение многочлена на линейные множители (6)
где х1, х2, … хn — это нули многочлена Разложение многочлена на линейные множители (6)
где х1, х2, … хn — это нули многочлена  . .
|
Если в равенстве (6) k чисел из набора х1, х2, … хn совпадают между собой и с числом a, то в произведении справа получается множитель (x – a)k. Тогда число x = a называется k-кратным корнем многочлена Pn(x), или корнем кратности k. Если k = 1, то число 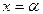 называется простым корнем многочлена Pn(x).
называется простым корнем многочлена Pn(x).
Например, 1) P4(x) = (x – i)4 Þ x = i — корень кратности 4;
2) P4(x) = (x – 2)(x – 4)3 Þ x1 = 2 — простой корень, x2 = 4 — трехкратный корень.
Дата добавления: 2015-10-19; просмотров: 1848;
