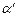Точная верхняя и точная нижняя грани множества
| Определения точной верхней грани и точной нижней граней множества точной верхней грани множества; точной нижней грани множества |
Пусть множество 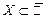 ограничено сверху. Наименьшее среди всех чисел, ограничивающих сверху это множество, называют точной верхней гранью множества(или просто верхней гранью) и обозначают
sup X (supremum — наибольший).
Если множество ограничено сверху. Наименьшее среди всех чисел, ограничивающих сверху это множество, называют точной верхней гранью множества(или просто верхней гранью) и обозначают
sup X (supremum — наибольший).
Если множество 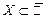 ограничено снизу, то наибольшее среди всех чисел, ограничивающих снизу это множество, называют точной нижней гранью множества(или просто нижней гранью) обозначается
inf X (infimum — наименьший). ограничено снизу, то наибольшее среди всех чисел, ограничивающих снизу это множество, называют точной нижней гранью множества(или просто нижней гранью) обозначается
inf X (infimum — наименьший).
|
По этому определению имеем, что число β = sup X, если выполняются следующие два условия:
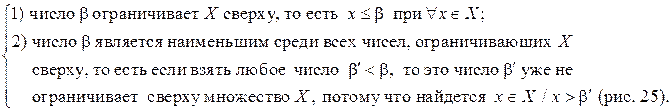
 Рис. 25
Рис. 25
| Þ | точную верхнюю грань множества нельзя подвинуть влево. |
Аналогично, число 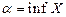 , если выполняются условия:
, если выполняются условия:


Рис. 26 | Þ | точную нижнюю грань множества нельзя подвинуть вправо. |
На рисунках 25 и 26 введены обозначения: множество 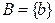 – это множество всех чисел, ограничивающих Х сверху, и множество
– это множество всех чисел, ограничивающих Х сверху, и множество  – это множество всех чисел, ограничивающих Х снизу. Очевидно, что
– это множество всех чисел, ограничивающих Х снизу. Очевидно, что 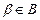 и
и 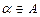 , но
, но 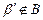 и
и 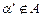 для
для 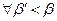 и для
и для 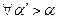 .
.
Учитывая этот разбор, можно записать наряду с данным выше описательным определением и формальное определение точных граней множества:
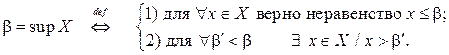
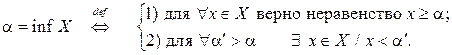
Пример 2 (определение точных граней множества)
1) 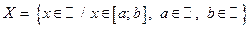 — ограничено сверху и снизу,
— ограничено сверху и снизу,
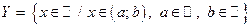 — ограничено сверху и снизу,
— ограничено сверху и снизу,

следовательно, точная нижняя и точная верхняя грани множества могут как принадлежать, так и не принадлежать самому множеству;
2) 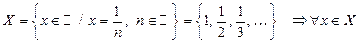 выполняется неравенство
выполняется неравенство 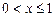
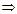 множество является ограниченным; sup X = 1, inf X = 0;
множество является ограниченным; sup X = 1, inf X = 0;
3) 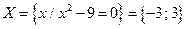 — ограниченное множество, sup X = 3, inf X = –3;
— ограниченное множество, sup X = 3, inf X = –3;
4)  — ограниченное множество, sup X = inf X = 5.
— ограниченное множество, sup X = inf X = 5.
Дата добавления: 2015-10-19; просмотров: 2085;