Методы одномерной оптимизации. Метод Ньютона.
Оптимизацией называют решение задачи по отысканию экстремальных значений функции. Точки экстремума функции 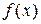 разыскиваются среди корней уравнения
разыскиваются среди корней уравнения 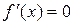 , а для функции
, а для функции  переменных
переменных 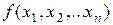 - среди решений системы
- среди решений системы
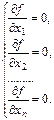
Пусть f(x) – дважды непрерывно дифференцируемая функция, причем f ''(x) > 0. Тогда, решение задачи минимизации функции f (x) сводится к решению нелинейного уравнения f '(x) = 0.
Метод Ньютона является наиболее эффективным методом решения нелинейных уравнений.
Пусть корень x* Î [a, b], так, что f '(a)f '(b) < 0. Положим x0 = b. Проведем касательную к графику функции y = f '(x) в точке B0 = (x0, f '(x0))
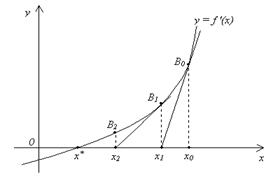
Рис. 1.5
Уравнение касательной будет иметь вид:
y – f '(x0) = f"(x0)(x – x0). (1.16)
Первое пересечение получим, взяв абсциссу точки пересечения этой касательной с осью OX, т. е. положив в (1.16) y = 0, x = x1:
x1 = x0 – 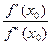 . (1.17)
. (1.17)
Аналогично поступим с точкой B1(x1, f '(x1)), затем с точкой B2(x2, f '(x2)), и т. д. в результате получим последовательность приближений x1, x2, …, xn , …, причем
xn +1 = xn – 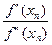 . (1.18)
. (1.18)
Формула (1.18) является расчетной формулой метода Ньютона.
При заданной точности e > 0 вычисления по формуле (1.18) нужно вести до тех пор, пока не будет выполнено неравенство | f '(xn)| £ e, после чего полагают x* » xn.
Дата добавления: 2015-10-19; просмотров: 1182;
