Теорема. (Достаточные условия экстремума).
Пусть в окрестности критической точки (х0, у0) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:
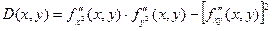
1) Если D(x0, y0) > 0, то в точке (х0, у0) функция f(x, y) имеет экстремум, если
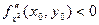 - максимум, если
- максимум, если 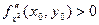 - минимум.
- минимум.
2) Если D(x0, y0) < 0, то в точке (х0, у0) функция f(x, y) не имеет экстремума
В случае, если D = 0, вывод о наличии экстремума сделать нельзя.
Пример. Исследовать функцию 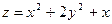 на экстремум.
на экстремум.
Находим частные производные первого порядка и приравниваем их к нулю:
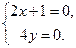
Стационарная точка данной функции имеет координаты 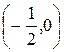 .
.
Вычислим вторые производные 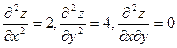 .
.
Следовательно, 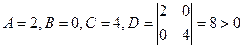 .
.
Экстремум имеется, т.к. 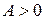 , то в точке
, то в точке 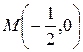 - минимум,
- минимум, 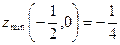 .
.
Метод множителей Лагранжа основан на том, что точка условного экстремума 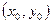 функции
функции 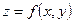 при условии
при условии 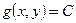 соответствует точке экстремума
соответствует точке экстремума 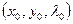 функции
функции 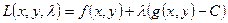 . Функция L называется функцией Лагранжа, а
. Функция L называется функцией Лагранжа, а 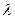 - множителем Лагранжа.
- множителем Лагранжа.
Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:
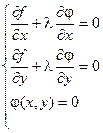
Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.
Пример. Найти экстремум функции f(x, y) = xy, если уравнение связи:
2x + 3y – 5 = 0

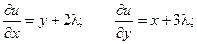
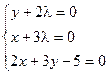
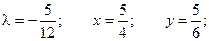
Таким образом, функция имеет экстремум в точке 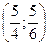 .
.
Дата добавления: 2015-10-19; просмотров: 701;
