Численное решение алгебраических уравнений. Метод Ньютона.
Пусть требуется решить уравнение 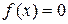 с точностью
с точностью 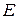 и
и 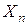 - приближенное значение корня. Воспользуемся формулой:
- приближенное значение корня. Воспользуемся формулой:
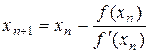 . (1)
. (1)
Если 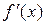 и
и 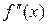 сохраняют свой знак в окрестности корня уравнения (строго положительны или строго отрицательны), то
сохраняют свой знак в окрестности корня уравнения (строго положительны или строго отрицательны), то 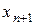 расположено ближе к корню, чем
расположено ближе к корню, чем 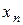 .
.
Циклическое повторение вычислений по формуле (1) при использовании на каждом последующем этапе найденного приближенного значения корня позволит вычислить корень со сколь угодно высокой точностью. Вычисления прекращаются, когда разность между соседними приближениями станет меньше Е. Данный метод решения уравнений называется методом Ньютона.
Пример 2. Найти корень уравнения 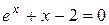 с точностью до 0,01 методом Ньютона.
с точностью до 0,01 методом Ньютона.
Используя графический метод (см. рис. 2), видим, что корень уравнения расположен на интервале (0;1)
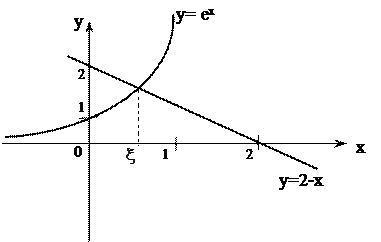 |
Рис. 2
В заданном уравнении 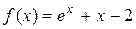 ,
, 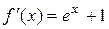 . Формула (1) для него имеет вид
. Формула (1) для него имеет вид
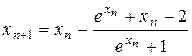 .
.
Из предыдущего примера известно, что корень уравнения расположен на интервале (0,1). Примем за начальное приближение 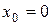 . Повторяя процесс вычислений, получим следующие значения
. Повторяя процесс вычислений, получим следующие значения
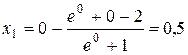 ,
,
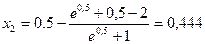 ,
,
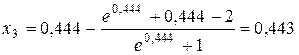 .
.
Так как 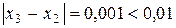 , то процесс вычислений заканчиваем, и корень уравнения считаем равным 0,443.
, то процесс вычислений заканчиваем, и корень уравнения считаем равным 0,443.
Дата добавления: 2015-10-19; просмотров: 685;
