Вероятность безотказной работы элементов

t, час	Р₁(t)	Р₂(t)	Р₂(t)	Р₃(t)	Р₄(t)	Р₅(t)

	0,980199		0,995696	0,9992	0,996918	0,972194
	0,960789	0,999994	0,995696	0,996805	0,987730	0,936745
	0,941765	0,999917	0,990256	0,992826	0,972604	0,894281
	0,923116	0,999532	0,983464	0,987282	0,951817	0,845456
	0,904837	0,998321	0,975087	0,980199	0,925741	0,790895
	0,886920	0,995466	0,964883	0,971611	0,894839	0,731242
	0,869358	0,989932	0,952605	0,961558	0,859646	0,667280
	0,852144	0,980612	0,938013	0,950089	0,820755	0,600058
	0,835270	0,966491	0,920884	0,937255	0,778801	0,530939
	0,818731	0,946799	0,901022	0,923116	0,734444	0,461577
	0,802519	0,921097	0,878275	0,907738	0,688351	0,393774
	0,786628	0,889326	0,852542	0,891188	0,641180	0,329303
	0,771052	0,851793	0,823788	0,873541	0,593567	0,269727
	0,755784	0,809123	0,792053	0,854875	0,546108	0,216247
	0,740818	0,762784	0,757456	0,835270	0,499352	0,169613
	0,726149	0,712001	0,720202	0,814810	0,453789	0,130105
	0,711770	0,659674	0,680578	0,793581	0,409845	0,097577
	0,697676	0,606303	0,595754	0,771669	0,367879	0,071540
	0,683861	0,552922	0,551479	0,749162	0,328179	0,051268
	0,670320	0,500461	0,506654	0,726149	0,290960	0,035911

На рис. 4 показаны графики функций P_i(t), i = 1,2,3,4,5, соответствующие вероятностям безотказной работы элементов. Номера графиков соответствуют номерам элементов. На рис. 5 изображен график вероятности безотказной работы системы Р_с(t).

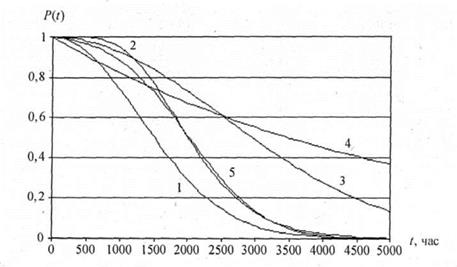
Рис. 4. Вероятность безотказной работы элементов

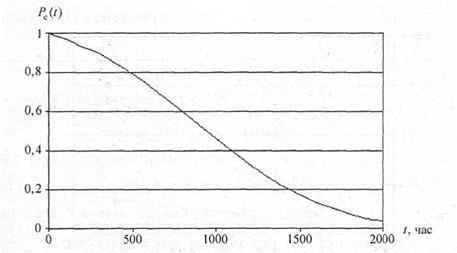
Рис. 5. Вероятность безотказной работы системы

Из графиков видно различное поведение вероятностей безотказной работы элементов. Скорость убывания вероятностей зависит от вида и параметров закона распределения. В нашем случае медленнее всего убывает P(t) для экспоненциального распределения и распределения Рэлея, т.e. при большом времени работы наиболее надежными оказываются третий и четвертый элементы системы.

Вычислим среднее время безотказной работы системы:

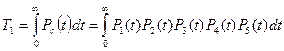
По формуле Симпсона:

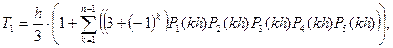
где n –число точек;

h – шаг интегрирования, выбираемый из условия обеспечения требуемой точности.

Расчеты показывают, что для данных табл. 7 T₁=976,3 час.

На рис. 6 изображены графики интенсивностей отказов элементов. Кривая 4, соответствующая экспоненциальном закону, параллельна оси времени, т. к. имеет постоянную интенсивность отказа. Все остальные кривые интенсивностей отказов являются возрастающими функциями времени.

На рис. 7 показан график интенсивности отказа системы, равной сумме интенсивностей отказов ее элементов:

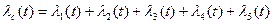
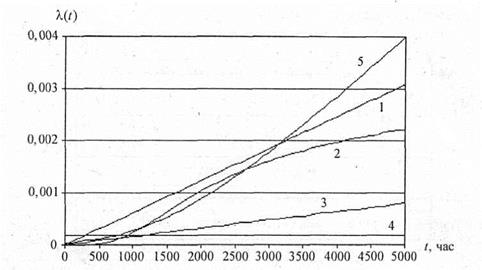
Рис. 6. Интенсивность отказов элементов

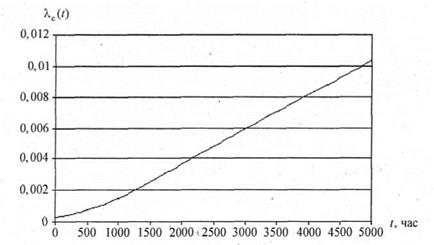
Рис. 7. Интенсивность отказа системы

Интенсивность отказа системы также является возрастающей функцией времени, что говорит о том, что система является стареющей, а закон распределения времени до ее отказа не экспоненциальный.

Вычислим плотности распределения вероятностей времени безотказной работы элементов.

Элемент 1. Распределение Вейбулла:

Элемент 2. Гамма-распределение:

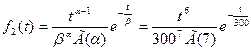
Элемент 3. Распределение Рэлея:

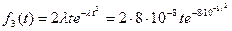
Элемент 4. Экспоненциальное распределение:

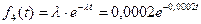
Элемента 5. Усеченное нормальное распределение:

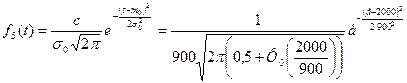
Табулируя плотности распределения от 0 до 2000 часов с шагом 100 часов, получим табл. 8.

Таблица 8

<21 22 232425 26 27 >

Дата добавления: 2015-09-07; просмотров: 1855;