Існування площини, паралельної даній площині

Доведення. Проведемо в даній площині α які-небудь дві прямі а й b, що перетинаються (мал. 16). Через дану точку А проведемо паралельні їм прямі а₁ і b₁. Площина β, що проходить через а₁ і b₁, по теоремі 2.4 паралельна площини α.

Припустимо, що через точку А проходить інша площина β₁ також паралельна площини α (мал. 17). Позначимо на площині β₁ довільну точку С, що не лежить у площині β. Проведемо площину γ через точки А, С и яку-небудь крапку В площини α. Ця площина перетне площини α, β і β₁ по прямим а, b і с. Прямі а й с не перетинають пряму b, оскільки не перетинають площину α. Отже, вони паралельні прямій b. Але у площині γ через точку А можна провести тільки одну пряму, паралельну прямій b. Ми прийшли до суперечності. Теорема доведена.

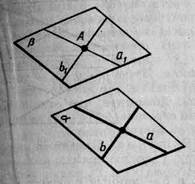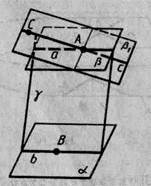Мал. 16 Мал. 17