Внутреннее эвольвентное зацепление

Если расположить начальную окружность малого колеса (шестерни) внутри начальной окружности большого колеса, то получим внутреннее зацепление. При этом полюс зацепления Р будет лежать вне линии центров [О₁О₂]. Угловые скорости обоих колес имеют одинаковый знак, т.к. зубчатые колеса вращаются в одну сторону. Поэтому передаточное отношение положительно:

U₁₂ = + ω₁/ω₂ = + z₂/z₁.

Построение профилей зубчатых колес при внутреннем зацеплении аналогично построению эвольвенты для внешнего зацепления. Поэтому все те способы, которые применялись для построения профиля, построения сопряженных точек, рабочей части профиля и др., можно целиком перенести на внутреннее зацепление. При этом нужно иметь в виду, что зуб внутреннего колеса имеет ряд особенностей – впадина внешнего зубчатого колеса будет заполняться телом зуба в колесе с внутренним венцом (рисунок 4.34).

Для внешнего колеса радиус окружности впадин будет больше, чем радиус окружности выступов R_f2 > R_a2. Активная линия зацепления ав будет находиться за пределами линии зацепления АВ и будет равна отрезку [Ра]. Также одной из особенностей внутреннего зацепления является возможность интерференции, т.е. наложение профиля колеса с внешним венцом на профиль колеса с внутренним венцом (рисунок 4.35). Это явление значительно усложняет расчет зубчатых колес с внутренним зацеплением.

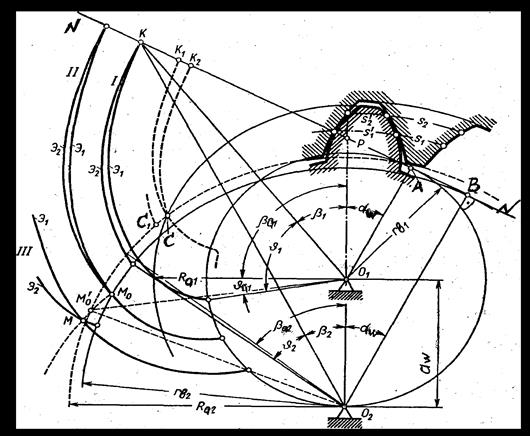
Рисунок 4.34 - Внутреннее эвольвентное зацепление

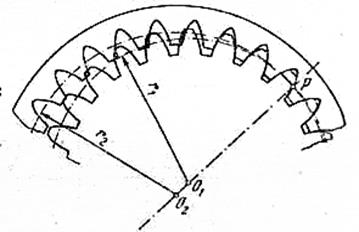
Рисунок 4.35 - Явление интерференции

При внутреннем зацеплении возможно подрезание ножки зуба малого колеса, если окружность выступов R_а2 второго колеса будет пересекать линию зацепления в пределах отрезка АВ или за точкой В.

Для выяснения геометрической картины интерференции представим себе профили колес, очерченные неограниченными эвольвентами Э₁ и Э₂, вращающимися при зацеплении колес вместе с начальными окружностями. В начале зацепления часть эвольвенты малого колеса между ее началом и точкой k зацепления располагается внутри соответствующей части эвольвенты большого колеса (позиция I, рисунок 4.34). При дальнейшем вращении эвольвента малого колеса сначала пройдет через начало эвольвенты 2-го колеса (позиция II, рисунок 4.34), а затем будет пересекать ее в точке М (позиция III, рисунок 4.34), которая меняет свое положение на неподвижной плоскости. Пересечение профилей в точке М соответствует теоретическому наложению профилей. Если высота головки зуба малого колеса такова, что окружность ее выступов пересекает кривую М вне участка М_оМ'_о, то будет наблюдаться наложение профилей. Явление интерференции будет отсутствовать при условии

R_a1< О₁М'_о.

Достоинства: 1) скорость скольжения меньше, чем при внешнем зацеплении с таким же модулем и числами зубьев; 2) более плавная и бесшумная работа; 3) коэффициент удельного скольжения меньше, а, следовательно, меньше изнашиваются зубья и более высокий КПД.

Недостатки: 1) чувствительность к изменению межосевого расстояния; 2) явление интерференции.