Внешнее эвольвентное зацепление
4.2.4.1 Эвольвента и ее свойства
Как указывалось в п. 4.2.1, профиль зуба может быть очерчен различными линиями. На практике широко применяется эвольвентное зацепление.
Эвольвентные передачи отличаются простотой и удобством изготовления зубьев, также допускают возможность изменения в известных границах межосевого расстояния передачи без нарушения правильности зацепления зубчатых колес. Профили зуба эвольвентного зацепления образуются двумя симметричными элементами.
Эвольвента – развертка круга. Эвольвента получается качением без скольжения нормали n-n по развертываемой окружности (рисунок 4.25). Окружность, по которой перекатывается прямая n-n, является эволютой. Т.о., эволюта – геометрическое место центров кривизны эвольвент, описываемых точками прямой n-n.
Рассмотрим построение эвольвенты. Пусть задана окружность радиусом R0 с центром в точке О (рисунок 4.25). Через точку М0 проведем прямую N0-N0, касательную к этой окружности, и будем катить эту прямую без скольжения. Для построения эвольвенты делим окружность от точки М0 на равные дуги: ◡ М0-1', ◡1'-2', ◡2'-3' и т.д. На прямой от точки М0 откладываем отрезки, равные дугам, т.е. [М0-1]=◡ М0-1', [1-2]=◡1´-2´ и т. д. Соединим точки 1', 2', 3' и т.д. с центром окружности О. К полученным радиусам проведем перпендикуляры, т.е. касательные к окружности N1, N2, N3. На них будем откладывать отрезки: на первой касательной от точки 1' откладываем отрезок [М0-1] – получаем точку М1; на второй касательной откладываем [М0-2] от точки 2' – получаем точку М2; на третьей касательной откладываем отрезок [М0-3] от точки 3' - получаем точку М3 и т.д. Соединяя полученные точки плавной линией, получаем эвольвенту круга.
4.2.1.4 Свойства эвольвенты
1. Нормаль, проведенная к сопряженным профилям, построенным по эвольвентам, всегда проходит через полюс зацепления р.
2. Нормаль, проведенная к любой точке эвольвенты, касательна к развертываемой окружности (Rb1, Rb2).
3. При увеличении радиуса основной окружности Rb эвольвента постепенно теряет свою кривизну; в пределе Rb1→ ∞ эвольвента превращается в прямую линию.
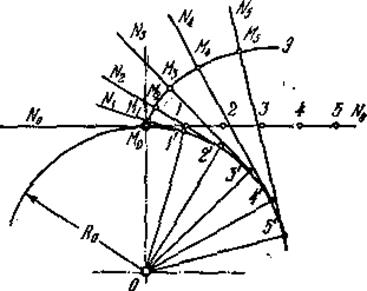
Рисунок 4.25 - Построение эвольвенты
Т.о., нормаль должна касаться соприкасаемых профилей и всегда проходить через полюс р. Из этих свойств вытекает, что эвольвентное зацепление обеспечивает постоянство передаточного отношения.
Нормаль к окружности проводится под углом α. Функция угла α называется эвольвентной функцией (инволютой) и обозначается сокращенно inv. Инволюта угла α равна углу J:
J = invα,
где J – радиус-вектор О1´´ любой точки эвольвенты, определяется по формуле
J = tgα – α.
Полученной функцией пользуются для аналитического определения радиус-вектора. Для удобства вычисления составлены таблицы invα для различных значений угла α.
4.2.4.2. Геометрические элементы зубчатых колес
Термины, определения и обозначения, относящиеся к геометрии и кинематике зубчатых передач различных типов с постоянным передаточным отношением, установлены ГОСТ 16530-83, зубчатых цилиндрических передач – ГОСТ 16531-83 и зубчатых конических передач – ГОСТ 19325-73. Основные термины и обозначения элементов, относящиеся к геометрии зубчатых передач, даны на рисунке 4.26.
Как было указано выше, два взаимоогибаемых профиля соединяются в точке полюса р. Профили двух круглых колес, которые соприкасаются в точке полюса р и перекатываются без скольжения, называются начальными окружностями. Радиусы этих окружностей обозначаются RW1 и RW2. Индекс «1» принадлежит первому колесу (шестерни), а индекс «2» принадлежит второму колесу.
Высота зуба h колеса состоит из головки зуба ha и ножки зуба hf:
h = ha+ hf. (4.24)
Окружность, которая делит зуб на головку и ножку, называетсяделительной (рисунок 4.26). Ее радиус обозначается R1, R2 и вычисляется по формуле:
R1 = mz1/2, R2 = mz2/2 = (мм), (4.25)
где z1, z2 - число зубьев шестерни и колеса; m - модуль зацепления.
Модуль – основная характеристика размеров зубчатых и червячных колес. Модули эвольвентных зубчатых колес стандартизованы ГОСТ 9563-60. Для колес, входящих в зацепление, модуль всегда одинаков! Зубья колес нарезаются на специальных станках режущим инструментом, размеры и форма которого зависит от величины модуля. Поэтому, ГОСТом установлены два ряда модулей, до которых должны округляться модули, получаемые расчетным путем:
1 ряд: 1,0; 1,25; 1,5; 2,0; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25.
2 ряд: 3,5; 4,5; 5,5; 7; 9; 11, 14, 18, 22, 28.
1-ый ряд предпочтительнее 2-го.
Модуль показывает, сколько раз число π укладывается в шаг Р
m = P/ π = (мм). (4.26)
Расстояние по делительной окружности между одноименными точками двух соседних зубьев называется шагом зацепления Р
P = π m = (мм). (4.27)
Шаг также складывается из толщины зуба и ширины впадины
P = S + e= (мм), (4.28)
где S - толщина зуба по делительной окружности, е - ширина впадины.
Так как шаг измеряется в мм, поэтому и модуль имеет размерность в мм.
Кроме шага по делительной окружности существуют также шаг по начальной окружности, шаг по основной окружности и т.д.
Для стандартного (нулевого) зацепления высота головки зуба равна модулю: ha = m, а высота ножки зуба равна hf = 1,25m.
Тогда высота зуба будет равна
h =2,25m.
Радиус, ограничивающий головку зуба, называется радиусом окружности выступов Ra(рисунок 4.26):
Ra1= R1 + m, Ra2 = R2 + m. (4.29)
Развертываемая окружность, с которой начинается построение эвольвенты, называется основной Rb
Rb1 = R1cosα, Rb2 = R2cosα, (4.30)
где α - угол зацепления.
Угол зацепления α – угол между линией зацепления АВ и прямой, перпендикулярной межосевой линии. Для стандартного (нулевого) зацепления α = 20о.
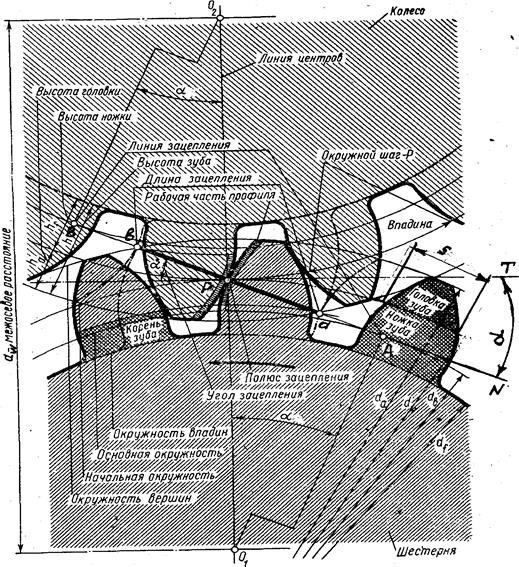
Рисунок 4.26 - Геометрические элементы зубчатого колеса
Радиус, ограничивающий впадину колеса, называется радиусом окружности впадинRf
Rf1= R1 - 1,25m, Rf2 = R2 - 1,25m. (4.31)
Для стандартного (нулевого) зацепления радиус начальной окружности совпадает с радиусом делительной (RW=R), толщина зуба равна ширине впадины и равна половине шага (S = e =1/2P) и, как указывалось выше, высота головки зуба равна модулю (ha=m), угол зацепления равен α = 20о.
Внимание! На рисунке 4.26 вместо радиусов указаны диаметры колес.
Межосевое расстояние вычисляется по формуле (4.16).
4.2.4.3. Построение эвольвентного внешнего зацепления
После расчета размеров элементов зубчатого зацепления (формулы 4.16, 4.24-4.31 и формулы из таблицы 4.2), откладываем межосевое расстояние aW. Из точки О1 проводим радиус начальной окружности шестерни R1, а из точки О2 – радиус начальной окружности колеса R2. Точка касания этих окружностей даст полюс зацепления р (рисунки 4.26, 4.27). Строим все остальные окружности: из точки О1 проводим радиусы с индексом «1», а из точки О2 – все радиусы с индексом «2». Через полюс проводим касательную к основным окружностям Rb1 и Rb2. Определяем точки касания. Для этого опускаем из точек О1 и О2 перпендикуляры на касательные и отмечаем точки: на окружности Rb1 - точку А, на окружности Rb2 - точку В. Отрезок АВ – линия зацепления.
Строим эвольвенту 1-го колеса, которую описывает точка Р прямой АВ при перекатывании ее по основной окружности. Отрезок [АР] делим на равные части (в данном примере на 4). Получаем точки 1, 2 и 3. Дугу основной окружности от точки А вправо делим на эти же части ([3-А] = È3¢А; [2-3] = È2¢3¢; [1-2]=È1¢2¢. Через точки 1¢, 2¢ и 3¢ проводим перпендикуляры в сторону полюса к соответствующим радиусам О11¢, О12¢ и О13¢, на которых откладываем отрезки [1¢-1¢¢]=[1-Р], [2¢-2¢¢]=[2-Р], [3¢-3¢¢]=[3-Р]. Соединяя полученные точки Р, 1¢¢, 2¢¢, 3¢¢плавной кривой, получаем эвольвенту части ножки колеса (левую часть зуба). Для построения нижней части ножки колеса нужно из точки 1¢¢ провести линию, параллельную межосевому расстоянию до радиуса окружности впадин и по окончании скруглить на величину радиального зазора. Строим эвольвенту головки зуба колеса. Для этого слева от точки А на линии зацепления АВ откладываем 2 одинаковых отрезка, равные отрезку [1-Р]. Получаем точки 5, 6. Такие же отрезки откладываем и на основной окружности также от точки А влево. Получаем точки 5¢ и 6¢. В дальнейшем выполняем аналогичные построения до тех пор, пока последняя точка не получится за пределами радиуса окружности выступов Ra.
Радиальный зазор с - расстояние между впадиной одного колеса и вершиной другого, т.е.:
с = aW - Ra1 - Rf2 = aW - Ra2 - Rf1 = 0,25m.
Если это расстояние не будет выдержано, то головка зуба одного колеса врежется в ножку зуба другого.
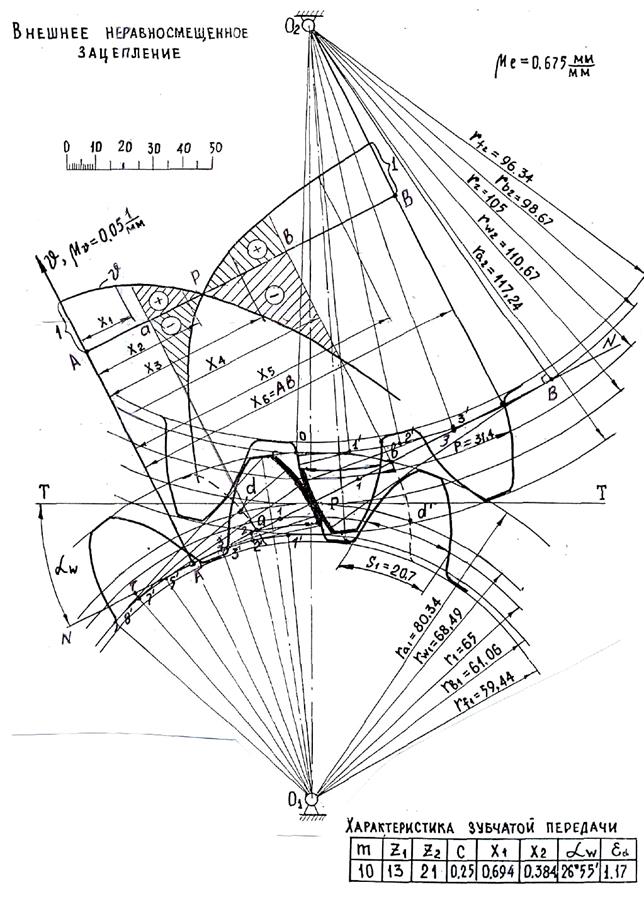
Рисунок 4.27 - Построение картины внешнего неравносмещенного
зацепления
Для построения левой стороны зуба, нужно отложить от точки С толщину зуба S1 по делительной окружности, получим точку D. Дугу СD делим пополам, получаем ось симметрии зуба. Вторую (правую) половину зуба можно построить двумя методами. 1-ый метод: провести несколько перпендикуляров к оси симметрии зуба и отложить на них замеренные с левой стороны расстояния. 2-ой метод: из твердой бумаги (картона) вырезать левую половину зуба и, перевернув его, построить правую половину. Чтобы построить 2-ой зуб, необходимо отложить шаг р от середины 1-го зуба по делительной окружности. Затем также по шаблону или геометрическим построением построить 2-ой зуб. Необходимо вычертить три зуба каждого колеса. Важно при построении выдерживать шаг и толщину зуба.
Для 2-го колеса построение 3-х зубьев осуществляется аналогично.
Достоинства эвольвентного зацепления. 1). Передаточное отношение в процессе движения профилей величина постоянная. 2). Передаточное отношение не зависит от изменения межосевого расстояния.
4.2.4.4 Линия зацепления. Дуга зацепления. Коэффициент перекрытия
Если зубчатым колесам сообщить вращение, то профили будут касаться в различных точках, при этом точка зацепления будет менять свое положение на неподвижной плоскости. Геометрическое место точек касания на неподвижной плоскости называется линией зацепления. Линия зацепления обозначается АВ и строится согласно п. 4.2.4.3.
Так как профили зубчатых колес ограничены окружностями головок, то линия зацепления используется частично. Часть линии зацепления находящаяся внутри ее, называется активной линией зацепления (отрезок ав). Построение активной линии заключается в пересечении линии зацепления АВ с окружностями выступов Ra1, Ra2.
Используя точки а и в, можно найти на профилях точки E и F, сопряженные с точками головки зуба соседнего колеса. Части EG и FH профилей являются рабочими участками зубьев. Вне этих участков зацепления не происходит и, следовательно, боковая поверхность в этих частях может ограничиваться произвольной кривой. Итак, рабочий профиль зуба – часть профиля зуба, который непосредственно участвует в зацеплении. Для его построения нужно провести дугу радиусом О2в до пересечения с профилем зуба 2-го колеса, сопряженным с профилем зуба 1-го колеса. Получается точка E. Аналогично строится рабочий профиль зуба шестерни (точка F).
Если представить положение двух сопряженных профиле в начале и в конце зацепления, то на начальных окружностях можно отметить точки а1, а2 в начале зацепления и точки а1, а2 в конце зацепления. Получается дуга зацепления – часть начальной окружности за время зацепления одной пары зубьев. Для нахождения дуги зацепления, нужно из концов рабочего профиля (из точек Е и F) в сторону вогнутости эвольвенты провести касательные к основным окружностям Rb1 и Rb2. На пересечении этих касательных с радиусами начальных окружностей RW1 и RW2 получаются точки а1, а2 и в1, в2, ограничивающие дуги зацепления. Длина дуги зацепления выражается через отношение длины активной лини зацепления ав к углу зацепления α:
ℓК = ℓав /cos α. (4.32)
Длина дуги зацепления всегда должна быть больше шага (ℓК>Р), в этом случае передача работает непрерывно, плавно без ударов:
ℓК /Р >1. (4.33)
Непрерывность работы зубчатой передачи должна обеспечиваться перекрытием одной пары зубьев другой, т.е. последующая пара зубьев должна войти в зацепление до выхода из зацепления предыдущей пары зубьев. В этом случае в зацеплении будет одновременно находиться не менее одной пары зубьев. Чем больше пар зубьев одновременно находится в зацеплении, тем более плавной будет работа зубчатой передачи. Плавность работы оценивается коэффициентом перекрытия – отношение длины дуги к шагу:
ξ =ℓК /Р =ℓав /πm cosα. (4.34)
С учетом сказанного выше, получаются следующие пределы коэффициента перекрытия для внешнего эвольвентного зацепления:
1,1 ≤ ξ ≤ 2.
Коэффициент перекрытия также может быть вычислен по следующей формуле:
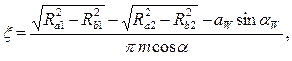 (4.35)
(4.35)
где αw – действительный угол зацепления, α – стандартный угол зацепления. Для нулевого (стандартного) зацепления αw = α = 200.
4.2.4.5 Коэффициент удельного скольжения зубьев
В процессе зацепления двух эвольвентных профилей наблюдается не только качение профиля по профилю, но и их скольжение друг по другу. В результате этого на участках рабочих профилей возникают силы трения. Это влияет на износ зубьев, уменьшает износостойкость передачи и ухудшает показатель работы зубчатой передачи. Для оценки взаимного скольжения профилей зубьев пользуются понятием коэффициента относительного скольжения зубьев λ – отношение скорости скольжения точек контакта зубьев к тангенциальным составляющим скоростей точек контакта сопряженных профилей:
λ = υск / υt.
Коэффициент удельного скольжения J связан с коэффициентом относительного скольжения λ через величину передаточного отношения U. При подсчете коэффициентов нужно иметь в виду, что если колеса разные, то зубья большего колеса зацепляются в U раз меньше, чем зубья малого колеса.
Исходя из этого для 1-го колеса J1 = λ1, а для 2-го J2 = λ2 / U12.
Коэффициенты удельного скольжения рассчитываются по формулам
J1 = 1- [(АВ-х)/(х·U12)]
J2= 1- [(х·U12) /(АВ-х)] (4.36)
где АВ – линия зацепления; х – расстояние от точки А касания линии зацепления с основной окружностью первого колеса, отсчитываемое в направлении к точке В. Диаграмма коэффициентов удельного скольжения строится в выбранном масштабе μJ (рисунок 4.28).
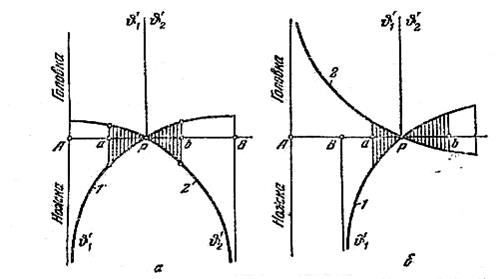
а - диаграмма для внешнего зацепления;
б - диаграмма для внутреннего зацепления.
Рисунок 4.28 - Диаграмма удельного скольжения зубьев
На рисунке 4.28 схематично показаны кривые изменения коэффициента удельного скольжения. По оси абсцисс откладывается теоретическая линия зацепления АВ. По оси ординат откладываются коэффициенты удельного скольжения J1 и J2, которые рассчитываются по формулам (4.36). Участки кривых, расположенные выше оси абсцисс, относятся к головкам зубьев, а участки, расположенные ниже оси абсцисс – к ножкам зубьев. Чтобы избежать больших потерь на скольжение профилей и уменьшить их износ, активная линия зацепления ав должна располагаться в зоне относительно малых коэффициентов скольжения (заштрихованная область на рисунке. 4.26 и 4.27).
4.2.4.6 Методы обработки цилиндрических зубчатых колес
Этот раздел достаточно хорошо освещен в источниках [1] и [3]. Мы коротко остановимся на основных методах обработки эвольвентных профилей, так как этот вопрос тесно связан с теорией профилирования зубьев.
Зубчатые колеса с эвольвентным профилем зубьев нарезаются на специальных зуборезных станках двумя методами: методом копирования и методом обкатки.
1. Метод копирования. Зубья нарезаемого колеса нарезаются на фрезерном станке специальной фасонной пальцевой фрезой или дисковой фрезой. Режущая кромка фрезы имеет очертание впадины между зубьями. Вращаясь, фреза перемещается в направлении боковой поверхности зуба. За каждый ход фрезы вдоль оси колеса получается нарезанной одна впадина. Затем фреза возвращается в исходное положение, а нарезаемое колесо поворачивается на угол β = 2π/z (рисунок 4.29, а,б). Точность этого способа изготовления колес невысока из-за возможного искажения профиля фрезы, неточности установки заготовки и инструмента и неточности деления. Применяют такие колеса для тихоходных и среднескоростных передачах.
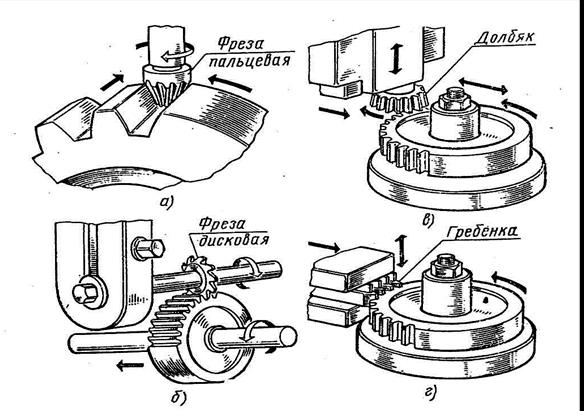
а – пальцевой фрезой, б - дисковой фрезой;
в - долбяком; г - инструментальной рейкой (гребенкой).
Рисунок 4.29 - Нарезание зубчатых колес
2. Метод обкатки. Режущим инструментом является точно изготовленное зубчатое колесо – долбяк. Долбяк совершает поступательное движение параллельно оси х-х нарезаемого колеса (рисунок 4.29, в). Одновременно колесу и долбяку совершается вращательное движение с тем же отношением угловых скоростей, как будто они находятся в зацеплении. Получается, что долбяк как бы обкатывает нарезаемое колесо. Эти методом можно нарезать и колеса с внутренним зацеплением.
Метод обкатки является более распространенным и совершенным методом. В основу этого метода лежат свойства зацепления сопряженных профилей. Достоинствами метода обкатки являются: универсальность инструмента, годного для изготовления зубчатых колес одного модуля всех чисел зубьев; большая точность воспроизведения профиля; простота изготовления и высокая степень точности инструмента, возможность изготовления колес как с внешним так и с внутренним венцом.
Методом обкатки можно нарезать колеса инструментальной рейкой (гребенкой) и червячной фрезой (рисунок 4.29, г).
Также колеса можно изготавливать литьем и штамповкой. Обычно эти методы применяются для изготовления колес из неметаллических материалов.
4.2.4.7 Подрезание профилей зубьев при изготовлении.
Минимальное число зубьев малого колеса
Во время изготовления зубчатых колес методом обкатки часто получается, что головка режущего инструмента врезается в ножку зуба нарезаемого колеса. В результате этого ножка зуба оказывается подрезанной, т.е. тоньше, чем головка зуба (рисунок 4.30, 6). Возникает явление подрезания. При подрезании ножка зуба ослабляется. При этом срезается часть эвольвенты, образующей профиль ножки зуба. Поэтому подрезание является нежелательным при изготовлении зубчатых колес.
Рассмотрим явление подрезания при нарезании колеса инструментальной рейкой (рисунок 4.30, в).
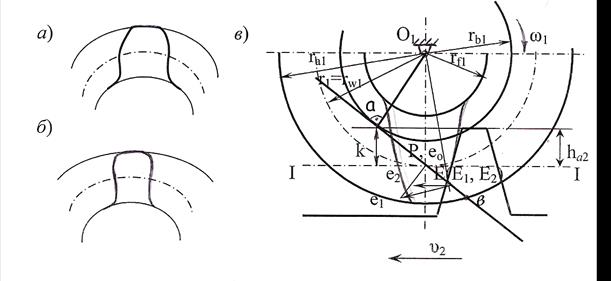
а - правильный зуб; б - подрезанный зуб;
в - явление подрезания при нарезании колеса.
Рисунок 4.30
При бесконечно большом диаметре делительной окружности зубчатое колесо превращается в рейку, а эвольвентный профиль зуба – в прямолинейный, удобный для изготовления и измерения. Возможность зацепления эвольвентного зубчатого колеса с рейкой имеет огромное практическое значение, так как позволяет изготовлять зуборезный инструмент в виде рейки с зубьями прямолинейной формы.
При нарезании колеса инструментальной рейкой сохраняются все свойства зацепления сопряженных профилей. Для реечного зацепления полюс зацепления Р получается в точке касания начальной окружности колеса rw1 и делительной прямой рейки I-I. Зуб колеса строится по правилам эвольвентного зацепления (п. 4.2.4.3. данной главы). Линия зацепления будет иметь только одну предельную точку – точку а, которая заключена между окружностью вершин колеса Ra1 и прямой вершин рейки. Чтобы имело место зацепление, необходимо, чтобы активная линия зацепления была меньше или равна линии зацепления, т.е. ав ≤ АВ. Если этого не происходит, т.е. ав >АВ, то не выполняется основной закон зацепления.
Рассмотрим явление подрезания. Примем, что ав = АВ, тогда точка а будет являться последней точкой зацепления. Скорость рейки υ2 всегда постоянна. Любая точка, которая расположена ниже точки а на зубчатом колесе, имеет скорость больше, чем скорость рейки, т.к. радиус контакта увеличивается. Выше точки а скорость колеса уменьшается по отношению к скорости рейки, т.к. радиус уменьшается (υ2 > υ1). Поэтому рейка надвигается на колесо быстрее, чем точки, расположенные выше точки а, надвигаются на рейку. Головка зуба рейки получается больше, чем ножка зуба колеса (ha2>hf1), и, поэтому рейка врезается в колесо. Так происходит подрезание зубьев. Явлением подрезания в теории зацепления называется пересечение окружностью вершин колеса при нарезании линии зацепления не далее АВ.
Выясним вопрос о наименьшем количестве зубьев малого колеса, при котором подрезание будет отсутствовать. Отметим точку Е – точку контакта колеса и рейки. Индекс «1» принадлежит колесу, а индекс «2» - рейки. Тогда в точке Е будут находиться две точки: точка Е1, принадлежащая колесу; и точка Е2, принадлежащая рейки. Отрезок [Ee1] – вектор скорости колеса, [Ee2] – вектор скорости рейки. Отметим точку k, для этого опустим перпендикуляр из точки а на делительную прямую рейки I-I. Отметим высоту головки зуба рейки ha2. Чтобы избежать подрезания зубьев, нужно, чтобы высота головки зуба рейки ha2 была меньше или равна отрезку [ak] и, чтобы скорость рейки была меньше, чем скорость колеса, т.е.:
ha2 ≤ [ak], υЕ2 < υЕ1. (4.37)
Рассмотрим треугольники ∆РО1Е и ∆Ее1е2, ∆Раk и ∆O1aP – они подобны по двум взаимно перпендикулярным сторонам:
∆РО1Е ~ ∆Ее1е2, ∆Раk ~ ∆O1aP.
Из треугольника ∆Раk имеем [аk] = [aP]sinα, из ∆O1aP имеем aP = [O1P]sinα. Подставим 2-ую формулу в первую, получим:
[аk] = [O1P]sin2α. (4.38)
Согласно условию (4.37), аk = ha2. Для стандартного зацепления ha2=m. Из рисунка 4.27 видно, что О1Р = R1. Тогда выражение (4.38) примет вид:
m = R1sin2α. (4.39)
Радиус делительной окружности вычисляется по формуле (4.25): R1 = mz1/2. Поэтому получаем следующее выражение, учитывая условие (4.37):
z1min ≥ 2/sin2α ≥17. (4.40)
Для стандартного зацепления α = 20о.
Формула (4.40) гласит: Для стандартного (нулевого) зацепления, чтобы избежать подрезания зубьев, нужно, чтобы число зубьев малого колеса было не менее 17.
Дата добавления: 2015-10-19; просмотров: 3775;
