Многозвенные зубчатые механизмы
При проектировании зубчатых механизмов возникает необходимость передавать вращение с большим передаточным отношением или при значительных межосевых расстояниях. В таких случаях применяют многозвенные зубчатые механизмы либо снижающие скорость вращения ведомого вала по сравнению с ведущим (редукторы), либо повышающие ее (мультипликаторы). Эти механизмы могут быть как плоскими, так и пространственными.
Многозвенные зубчатые механизмы – механизмы, состоящие из простейших зубчатых механизмов, общее передаточное отношение которых рассчитывается по формуле (4.20). Они бывают с неподвижными осями (цилиндрические, конические, червячные редукторы) и с подвижными осями (планетарные и дифференциальные редукторы).
4.2.8.1 Многозвенные механизмы с неподвижными осями
Как указывалось в п. 4.2.1, простейшим зубчатым механизмом является одноступенчатый редуктор (рисунок 4.20, а). Если зубчатый механизм имеет более одной ступени, то он является многозвенным (многоступенчатым).
Проектирование многоступенчатых редукторов заключается в подборе по заданному общему передаточному отношению основных размеров колес и их чисел зубьев. При этом необходимо учитывать и некоторые дополнительные условия, связанные с конструктивными требованиями. Например, если оси колес 1 и 3 расположены на одной оси, то такой редуктор является соосным (рисунок 4.38, б) и для него должно выполняться условие соосности:
r1+ r2 = r2¢+ r3 или z1+ z2 = z2¢+ z3.
|
а - несоосный; б - соосный; в - соосный с внешним
и внутренним зацеплением.
Рисунок 4.38 - Двухступенчатые цилиндрические редукторы
Разновидностей многоступенчатых редукторов очень много. Многозвенные механизмы могут проектироваться в сочетании цилиндрического и конического редукторов, цилиндрического и червячного редукторов и др. Это необходимо для уменьшения габаритных размеров механизмов.
Более подробно проектирование многоступенчатых цилиндрических редукторов рассматривается в курсе «Детали машин».
4.2.8.2 Многозвенные механизмы с подвижными осями
Многозвенные зубчатые механизмы с подвижными осями могут быть как с жесткими колесами (планетарные редукторы), так и с гибкими (волновые передачи).
Достоинством механизмов с подвижными осями является их ощутимая компактность по сравнению с механизмами с неподвижными осями, более высокий КПД и большое передаточное отношение.
Планетарные механизмы подразделяются на:
Ø планетарные редукторы и мультипликаторы (рисунок 4.39, а) – зубчатые механизмы с подвижной осью вращения, которые имеют опорное колесо и обладают одной степенью подвижности W = 1.
Ø дифференциальные механизмы (рисунок 4.39, б) – со степенью подвижности W = 2 или более и которые не имеют опорного колеса.
Планетарные и дифференциальные механизмы изготавливают, как правило, соосными.
Рассмотрим структуру планетарного редуктора (рисунок 4.39, а).
Колеса с подвижными осями вращения называются планетарными или сателлитами (z2). Звено, на котором располагаются оси сателлитов называется водилом (на кинематических схемах водило обозначается буквой Н). Зубчатое колесо с неподвижной осью вращения называется солнечным или центральным (z1). Неподвижное колесо называется опорным (z3).
|
|
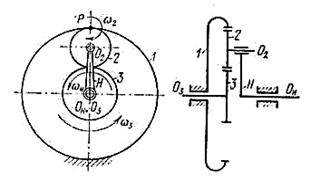
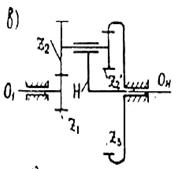
а - планетарный механизм; б - дифференциальный механизм.
Рисунок 4.39. - Механизмы с подвижными осями
Степень подвижности планетарного редуктора равна 1 (W = 3n - 2p5 - p4 = 3×2-2×2-1 = 1). Поэтому редуктор имеет постоянное передаточное отношение.
Если в рассмотренном механизме освободить от закрепления опорное колесо z3 сообщить ему вращение, то все центральные колеса станут подвижными и механизм превратиться в дифференциальный (рисунок 4.39, б), т.к. степень подвижности его будет равна 2 (W = 3n - 2p5 - p4 = 3×4 - 2×4 - 2 = 2). Наоборот, любой дифференциал можно превратить в планерный редуктор, если закрепить его одно или несколько центральных колес. Это свойство планетарных редукторов носит название свойства обратимости. Оно позволяет применять одинаковые методы исследования и проектирования для планетарных редукторов и для дифференциалов.
4.2.8.3 Кинематика планетарных редукторов
Передаточное отношение любого зубчатого механизма рассчитывается по формуле (4.15):
U12 = ω1/ω2 = r2/r1 = z2/z1.
Определим передаточное отношение планетарного редуктора (рисунок 4.40, а). Скорость точки О2 одинакова для колеса и водила:
VH = VO2 = ω2r2 = - ωH (r3-r2).
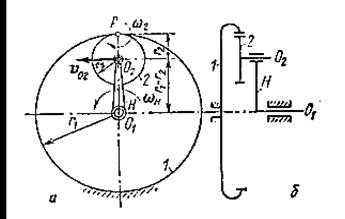
Рисунок 4.40. - К определению передаточного отношения
планетарного редуктора
Так как 3-е колесо неподвижно (опорное), то передаточное отношение от 1-го колеса к водилу будет вычисляться по формуле:
U1Н =ω1/ωН = (r1-r3)/r1 = 1- r3/r1 = 1-U13.
Или U31Н = 1 - UН13. (4.49)
Переставив слагаемые, получим:
U31Н + UН13 = 1. (4.50)
Формула (4.50) гласит:сумма передаточных отношений в планетарном механизме при любых останавливаемых звеньях всегда равна 1.
В формуле (4.50) верхний индекс указывает индекс неподвижного звена. Тогда U31Н - передаточное отношение 1-го колеса к водилу Н при неподвижном колесе 3; UН13 - передаточное отношение 1-го колеса к 3-му при неподвижном водиле Н.
Определим передаточное отношение через числа зубьев. Для планетарного редуктора (рисунок 4.39, а) по формуле (4.50) имеем
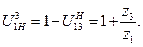(4.51)
Для дифференциального редуктора (рис. 4.39, б)
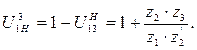(4.52)
Определим передаточное отношение дифференциального редуктора через угловые скорости (рисунок 4.39, б).
Пусть звенья, входящие в кинематические пары со стойкой, движутся с угловыми скоростями ω1, ω3 и ωН. Сообщим всем звеньям механизма дополнительное вращение вокруг оси ОН с угловой скоростью «-ωН», равной по величине и противоположной по направлению. Тогда звенья механизма будут иметь скорости:
ω1Н = ω1 - ωН
ω3Н = ω3 - ωН (4.53)
ωНН = ωН - ωН = 0.
Передаточное отношение от 1-го звена ко 2-му рассчитывается по формуле:
UН13= ω1Н/ ω3Н. (4.54)
Подставляя выражения (4.53) в формулу (4.54), имеем:
UН13 =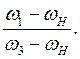 
Эту формулу можно обобщить для дифференциального механизма с любым числом колес до n:
UН1n=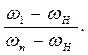 
(4.55)
Выражение (4.55) носит название формулы Виллиса для определения передаточного отношения дифференциального редуктора. Угловая скорость ω2 не входит в эту формулу, т.к. колесо 2 является паразитным.
Механизмы дифференциалов широко применяются в автомобилях, счетных машинах, сельскохозяйственных машинах и т.д. Широкое распространение получили конические планетарные механизмы.
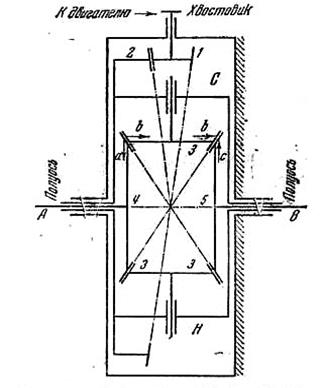
а - схема конического автомобильного дифференциала;
б - положение колес автомобиля при повороте.
Рисунок 4.41
На рисунке 4.41, а показан конический дифференциал, применяемый в автомобилях. При повороте ведущих колес автомобиля (рисунок 4.41, б) колесо 1, катящееся во внешней кривой α-α, должно пройти больший путь, чем колесо 2, катящееся по внутренней кривой β-β. Следовательно, скорость колеса 1 оказывается больше, чем колеса 2. Чтобы воспроизвести это движение колес с различными угловыми скоростями, и применяется дифференциал.
Коническое зубчатое колесо 1 (рисунок 4.41) получает вращение от двигателя. Это зубчатое колесо входит в зацепление с коническим зубчатым колесом 2, вращающимся свободно на полуоси А. С колесом 2 скреплена коробка Н, служащая водилом. В коробке Н свободно на своих осях вращаются два одинаковых сателлита 3. Сателлиты 3 находятся в зацеплении с двумя одинаковыми зубчатыми колесами 4 и 5, скрепленными с полуосями А и В. Если колеса автомобиля двигаются по прямым, то можно считать, что моменты сил сопротивления на осях А и В равны и, следовательно, сателлиты 3 находятся относительно их собственных осей вращения в равновесии, и они не поворачиваются вокруг своих осей. Тогда коробка Н вместе с сателлитами 3 и полуоси А и В вращаются как одно целое в одну и ту же сторону с одинаковой угловой скоростью. Как только колеса автомобиля начнут двигаться по кривым различных радиусов R1 и R2 (рисунок 4.41, б) сателлиты 3 начнут поворачиваться вкруг своих осей, и весь механизм будет работать как дифференциальный механизм.
Рассмотрим кинематику дифференциала. Передаточное отношение согласно формуле (4.55) будет иметь вид:
UН45=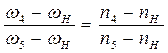 
, (4.56)
где n4 и n5 – числа оборотов в минуту коле 4 и 5; nH – число оборотов коробки Н (водила). Колесо 4 входит в зацепление с паразитными колесами 3 (сателлитами), которые в свою очередь сцепляются с колесом 5, одинаковым с колесом 4.
UН45=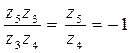 
. (4.57)
Знак минус поставлен потому, что колеса 4 и 5 вращаются в разные стороны. Тогда окончательно имеем
UН45=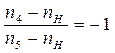 
. (4.58)
Разновидностей планетарных редукторов очень много. В нашу задачу не входит рассмотрение их структуры. Мы же должны сделать упор на синтезе (проектировании) зубчатых механизмов с подвижными осями.
4.2.8.4 Особенности проектирования планетарных редукторов
Проектирование зубчатых механизмов заключается в подборе основных размеров колес и числа их зубьев по заданному общему передаточному отношению U31Н.
При проектировании планетарных редукторов должны учитываться следующие условия:
Ø условие соосности;
Ø условие соседства сателлитов;
Ø условие сборки;
Ø заданное передаточное отношение;
Ø заданный модуль m;
Ø отсутствие заклинивания колес передачи.
Кроме того, для стандартных колес необходимо, чтобы отсутствовало подрезание зубьев, а для внутреннего зацепления отсутствовала интерференция зубьев. При этом необходимо выполнение следующих условий:
1. количество чисел зубьев 1-го колеса с внешним венцом должно быть не менее 17 (z1 ≥ 17);
2. количество чисел зубьев 3-го колеса с внутренним венцом должно быть не менее 85 (z3 ≥ 85);
3. числа зубьев колес z1 и z3 должны быть одинаковой четности.
Условие соосности необходимо, чтобы оси колес z1 и z3 располагались на одной оси, благодаря чему обеспечивается зацепление сателлитов с центральными колесами. Для планетарного редуктора с центральным колесом (рисунок 4.39, а) необходимо выполнение условия:
r1+2r2 = r3 или z1+ 2z2 = z3. (4.59)
Для дифференциального редуктора (рисунок 4.39, б) условие соосности имеет вид
z1+ z2 = z3 - z2¢. (4.60)
Условие соседства – условие совместного размещения нескольких сателлитов по общей окружности в одной плоскости. В редукторах для уменьшения нагрузок на зубья колес, с целью уменьшения габаритов, и из условий требований к динамической уравновешенности водила, устанавливают не один, а несколько сателлитов. Эти сателлиты устанавливаются под равными углами в одной плоскости и радиусы окружностей выступов сателлитов не должны пересекаться. На рисунке 4.42 показаны сателлиты 2 и 2''' в предельном соседстве, когда окружности их головок радиусов Ra2 и Ra3. Из треугольника АВС следует: чтобы радиусы окружностей выступов не соприкасались, необходимо соблюдения следующего неравенства:
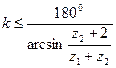. (4.61)
где k – число сателлитов.
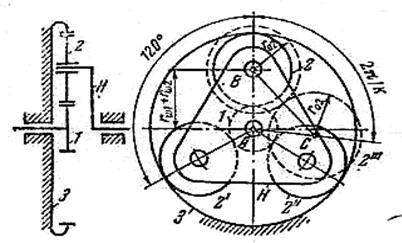
Рисунок 4.42 - К подбору сателлитов
Условие сборки (собираемости) – при равных углах между сателлитами учитывается необходимость одновременного зацепления всех сателлитов с центральными колесами при симметричной геометрии зон зацепления. После установки первого сателлита подвижное центральное колесо принимает строго определенное положение. И если не выполнить некоторых требований, то при установке следующих сателлитов их зубья могут не оказаться точно против впадин одного из центральных колес и тогда осуществить сборку механизма невозможно. При сборке планетарного редуктора первый поставленный сателлит полностью определяет взаимное расположение центральных колес. Условие сборки является проверкой условий соосности и соседства:
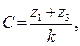, (4.62)
где k – число теоретически возможных сателлитов, С - некоторое (целое!) число. Числа зубьев должны быть подобраны так, чтобы число сателлитов k получилось целым. Уравнения (4.61) и (4.62) нужно учитывать одновременно. Также необходимо, чтобы числа зубьев z1 и z3 имели одинаковую четность.
Пример 1. Подобрать числа зубьев z1, z2 и z3 для передачи (рисунок 4.39, а) с передаточным отношением U1H =5,6 и определить количество сателлитов k.
Задаемся числом зубьев z1, из ряда z1 =17, 18, 19, 20…
Пусть z1 =18. Число зубьев z3 найдем из выражения (4.54):
U1H(3)-1=z3/z1, откуда z3=z1(U1H-1)=18(5,6-1)=82,8.
Условие z3 ≥ zmin=85 не выполняется, поэтому задаемся новым числом зубьев z1. Пусть z1=19, тогда
z3=z1(U1H-1)=19(5,6-1)=87,4.
Округляем z3 до целого, чтобы z3 было бы одинаковой четности с z1, т.е. z3=87. Из условия соосности (4.59) найдем z2
z2=(z3-z1)/2=(87-19)/2=34.
Из условия соседства (4.61) определяем возможное число сателлитов в механизме
k ≤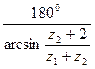 
≤ 
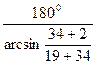≤ 4,2.
Значит, для этого механизма число сателлитов может быть взято равное 2, 3 и 4. Принимаем k = 4. Проверяем условие сборки из выражения (4.62)
(z1+z3)/k= C, (19+87)/4=26,5.
Число в ответе получилось не целое, значит, при этих числах зубьев механизм без натягов не соберется. Назначаем новое число z1. Пусть z1=20, тогда
z3=z1(U1H-1)=20(5,6-1)=92, z2=(z3-z1)/2=(92-20)/2=36.
Находим возможное число сателлитов из условия (4.61)
k ≤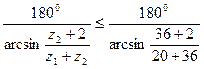 
≤4,2.
Принимаем k = 4 и проверяем условие сборки по формуле (4.62)
.
Тогда (20+92)/4 = 28.
Все условия выполняются, значит, окончательно принимаем
k = 4, z1 = 20, z2 = 36, z3 = 92.
Пример 2 (рисунок 4.39, б). Подобрать числа зубьев z1, z2, z¢2 и z3 для передачи с передаточным отношением U1H =10,18 и определить количество сателлитов k. Из выражения (4.52) находим
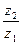
= U1Н -1=10,18-1=9,18.
Передаточное отношение многоступенчатых редукторов равно произведению передаточных отношений отдельных ступеней (4.22)
U1n=U12∙U23∙…∙U(n-1)n.
Согласно выражению (10) находим
z2/z1=U12H, z3/z2'=U23H.
Пусть U12H=3, значит, U23H=9,18/3=3,06. Тогда z2=3z1 и z3=3,06 z2'. Задаемся числом зубьев z1. Из условия (►2.) (см. выше) z1 нужно выбирать из ряда 17, 18, 19, 20…. Пусть z1=17, тогда z2 = 3·17 = 51. Запишем условие соосности (4.57)
z1 + z2 = z3 - z2'.
Из условия (4.57) найдем z2:
17+51 = 3,06 z2'-z2', т.е. 68 = 2,06z2'.
Откуда z2’= 33,0097. Принимаем z2'=33, тогда z3=3,06·33=100,98. Округляем z3 до целого, чтобы z3 было бы одинаковой четности с z1, т.е. принимаем z3 = 101. Определяем число сателлитов
k ≤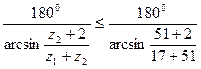 
≤ 3,515.
Значит, в схеме механизма может быть либо 2, либо 3 сателлита. Принимаем k=3. Проверяем, возможна ли сборка механизма по условию:
,
тогда (17+101)/3=39,33 - число не целое, значит, механизм без натягов не может быть собран. Назначаем новое число зубьев z1=18, тогда z2=3·18=54. Из условия соосности (4.57) найдем
z2'·2,06z2'=18+54=72, z2'=34,95.
Принимаем z2'=35, тогда
z3=3,06 z2'=3,06·35=107,1.
Принимаем z3=108, чтобы z3 было бы одной четности с z1. Определяем возможное число сателлитов k
k ≤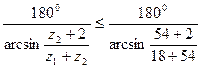 
≤ 3,6,
т.е. получим тот же результат, что и при z1=17. Проверяем возможность сборки из условия (4.62)
,
тогда (108+18)/3=42. Число в ответе целое, значит, сборка механизма возможна.
Итак, окончательно имеем: k=3, z1=18, z2=54, z2'=35, z3=108.
Пример 3. Определить число зубьев 2-го колеса z2 и количество сателлитов k, если заданы числа зубьев z1=20, z3 = 70 (рисунок 4.39, а).
Решение. Из условия соосности (4.59) имеем
z2 = (z3 - z1)/2 = (70-20)/2 = 25.
По условию соседства (4.60), получаем
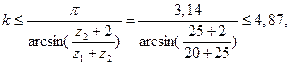
т.е. число сателлитов должно быть не более k ≤ 4. И, наконец, из условия сборки (4.61), имеем:
.
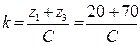Так как числа k и С должны быть целыми, то при выборе k = 4 условие (4.61) не может быть удовлетворено. Условию сборки удовлетворяет число сателлитов k = 3. Тогда С = 30.
Итак, z2 = 25 и k = 3.
Если задан модуль, можно также определить радиусы окружностей и межосевое расстояние (таблица 4.2).
Вопросы для самоконтороля
1. Чему равна степень свободы планетарного механизма, дифференциального механизма?
2. В чем заключается метод обращения движения и где он используется?
3. Напишите формулу Виллиса и поясните, для определения передаточного отношения каких механизмов можно ее использовать?
4. Напишите условие соосности для простейших схем планетарных механизмов.
5. Напишите условия соседства и сборки и поясните их физический смысл.
Мы рассмотрели основные задачи кинематического и динамического анализа, а также синтез типовых рычажных, кулачковых и зубчатых механизмов. В данном пособии не рассматривается проектирование механизмов с использованием ЭВМ и компьютерных программ. Этому вопросу посвящены отдельные издания по теории механизмов и машин (см. источники [8], [9]).
Дата добавления: 2015-10-19; просмотров: 2150;