Минимальная сумма зубчатых колес
При конструировании машин стремятся к уменьшению габаритных размеров зубчатой передачи без уменьшения прочности зубьев. При расчете зубчатых колес это приводит к уменьшению суммы чисел зубьев, т.к. межосевое расстояние пропорционально сумме (z1+z2)
aW = m(z1+z2)/2.
Модуль зацепления определяется передаваемой нагрузкой. Полностью используя отрезок АВ линии зацепления в качестве рабочей части, можно легко найти наименьшую сумму чисел зубьев, при которой коэффициент перекрытия ξ = 1,1 и подрезание зубьев отсутствует. Рассмотрим рисунок 4.31.
|
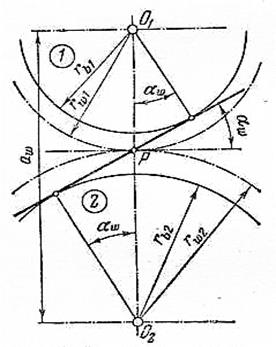
Примем, что линия зацепления равна активной линии, т.е.:
АВ = ав (4.41)
Из рисунка 4.31 видно, что
АВ = АР + РВ. (4.42)
АР = О1Р sinα, РВ = О2Р sinα.
Тогда получаем
АВ = О1Р sinα + О2Р sinα,
где О1Р = R1=mz1/2; O2P=R2=mz2/2.
Выражение (4.42) примет вид
АВ = mz1sinα/2 + mz2sinα/2.
С учетом выражения (4.44) имеем:
ℓав = [m(z1+ z2)sinα]/2 (4.43)
Коэффициент перекрытия ξ вычисляется по формуле 4.37
ξ = ℓав /πm cosα .
Подставим это выражение в формулу (4.43), получим:
ξ =[m(z1+ z2)sinα] /2πm cosα.
Выразим минимальную сумму колес с учетом, что ξ = 1,1
(z1+ z2)min = 2,2π/tgα.
Если ξ ≥1,1, то для каждой передачи должно удовлетворяться неравенство:
(z1+ z2)min ≥ 2,2π/tgα. (4.44)
Для стандартного (нулевого) зацепления (при α = 20о) минимальная сумма должна быть больше или равна 18:
(z1+ z2)min ≥18. (4.45)
Таким образом, чтобы имело место зацепление при отсутствии подрезания колес, нужно, чтобы удовлетворялось неравенство (4.45). Для нулевого же зацепления минимальная сумма должна быть больше 18 или равна ей.
4.2.4.9 Корригирование зубчатых колес
Профилирование зубьев эвольвентного зацепления и инструмента для нарезания осуществляется в соответствии с исходным контуром, т.е. контуром зубьев номинальной исходной рейки в сечении плоскостью, перпендикулярной ее делительной поверхности. Исходный контур цилиндрических эвольвентных зубчатых колес с модулем m ≥ 1 мм стандартизован ГОСТ 13755-81, а конических зубчатых колес с прямыми зубьями – ГОСТ 13754-81. Профиль того и другого контура является прямолинейным, расположенным на одинаковой длине по обе стороны от средней линии I-I, по которой толщина зуба и ширина впадины равны. Расстояние между одноименными профилями двух соседних зубьев, измеряемое параллельно средней линии, называется шагом рейки р.
Отношение высоты головки зуба к модулю называется коэффициентом высоты головки зуба
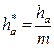 .
.
Отношение величины радиального зазора к модулю называется коэффициентом радиального зазора
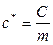 .
.
По ГОСТ 13755-81 и ГОСТ 13754-81 параметры исходного контура: угол профиля α = 200; глубина захода зубьев hw = 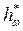 m (
m ( 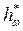 - коэффициент глубины захода зубьев); коэффициент высоты головки зуба
- коэффициент глубины захода зубьев); коэффициент высоты головки зуба 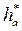 =1; коэффициент радиального зазора для цилиндрических зубчатых колес с* = 0,25 (при обработке долбяком и шеверами до с* = 0,35, до с* = 0,4 при шлифовании зубьев) и для конических зубчатых колес с* = 0,2; радиус закругления зуба у основании цилиндрических зубчатых колес r0 = 0,38m и конических зубчатых колес r0 = 0,2m.
=1; коэффициент радиального зазора для цилиндрических зубчатых колес с* = 0,25 (при обработке долбяком и шеверами до с* = 0,35, до с* = 0,4 при шлифовании зубьев) и для конических зубчатых колес с* = 0,2; радиус закругления зуба у основании цилиндрических зубчатых колес r0 = 0,38m и конических зубчатых колес r0 = 0,2m.
Зубчатые колеса с геометрическими элементами, отличающимися от стандартных (с углом зацепления α ≠ 20о, высотой головки зуба ha ≠ m, с модулем, отличным от стандартного значения), называются корригированными, т.е. исправленными в каком либо отношении. Корригирование зубчатых колес необходимо, чтобы избежать подрезания зубьев. Корригированные зубчатые колеса (передачи со смещением) позволяют
1. Улучшить условия работы зубьев – увеличить прочность, уменьшить наибольшее значение удельного скольжения.
2. Улучшить качественные характеристики зацепления – повысить несущую способность за счет утолщения ножки зуба, увеличить радиус кривизны, уменьшить число зубьев, увеличить модуль.
3. Вписать передачу в заданное межосевое расстояние.
Рассмотрим нарезание зубчатых колес инструментальной рейкой. У стандартной рейки, так же как и у стандартного колеса (рисунок 4.32), угол равен α W = 20о, толщина зуба S равна ширине впадины е (S = е). Делительная прямая рейки I-I также делит зуб на ножку и головку, но высоты их равны (ha2 = hf2).
При нарезании стандартного (нулевого) колеса модульная прямая рейки совпадает с делительной прямой (рисунок 4.32).
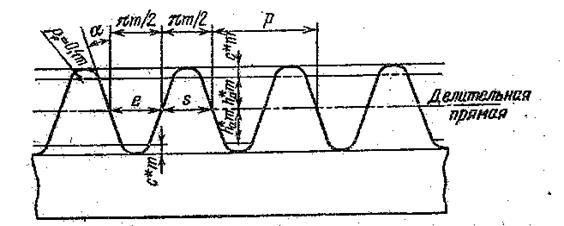
Рисунок 4.32 - Инструментальная рейка
Рейку в процессе нарезания можно расположить так, что модульная прямая не будет совпадать с делительной прямой, при этом толщина зуба и ширина впадины получаются неодинаковыми, хотя шаг остается прежним. Также не меняются эвольвента и радиус основной окружности нарезаемого колеса. Рейка в процессе нарезания смещается на величину а, которое носит название величины абсолютного смещения – расстояние между делительной и модульной прямыми рейки. Она вычисляется по формуле:
а = χm, (4.46)
где m - модуль зацепления, χ – коэффициент смещения (относительный сдвиг рейки) – отношение абсолютного смещения рейки к модулю:
χ = а/m. (4.47)
Для стандартного зацепления
χ = (17-z)/17. (4.48)
Минимальный относительный сдвиг стандартной рейки при нарезании колес с числом зубьев z < 17 называется положительным, т.е. рейка отодвигается от центра нарезаемого колеса, а при нарезании колес с z > 17 – отрицательный, т.е. рейка может быть придвинута к центру колеса.
В зависимости от числа зубьев и вида смещения рейки, В.Н. Кудрявцевым разработаны таблицы, по которым можно легко определить коэффициенты смещения. Таблицы приведены в конце данного пособия.
Виды зубчатых колес в зависимости от смещения рейки
В зависимости от сдвига рейки колеса бывают:
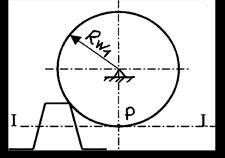
Рисунок 4.33, а. Нулевое колесо
1. Нулевые – стандартные колеса (рисунок 4.33 а), когда абсолютное смещение равно нулю, толщина зуба равна ширине впадины и равна половине шага, высота головки зуба равна модулю, угол зацепления равен 20о (а=0, S=e =1/2P, ha= m, α =20o).
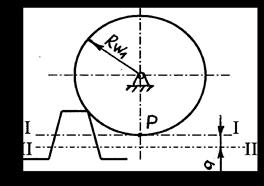
Рисунок 4.33, б - Положительное колесо
2. Положительные – смещение рейки направлено в сторону от оси нарезаемого колеса (рисунок 4.33, б). Толщина зуба при этом получается больше, чем ширина впадины (S > e) и, следовательно, больше половины шага (S>1/2P).
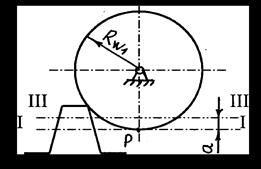
Рисунок 4.33, в. - Отрицательное колесо
3. Отрицательные – смещение рейки направлено к оси нарезаемого колеса (рисунок 4.33, в). При этом толщина зуба получается меньше, чем ширина впадины (S < e) и, следовательно, меньше половины шага (S < 1/2P).
Типы зубчатых передач в зависимости от смещения рейки
В зависимости от типов зубчатых колес зубчатые передачи бывают:
1. Стандартная (нулевая) зубчатая передача – оба колеса нарезаны без смещения (χ1 = χ2 = 0), S = e = 1/2P, действительный угол зацепления равен стандартному углу (αW =α =20o).
2. Равносмещенная зубчатая передача – составлена из положительного (шестерня) и отрицательного зубчатого колеса с коэффициентами смещения, равными по абсолютной величине (χ1= - χ2). При такой передаче, толщина зуба шестерни S1 становится больше, чем ширина впадины е1, а у 2-го колеса наоборот. Также выполняются условия: S1 = e2, S2 = e1, S1 + S2 = P, αW = α =20o.
3. Неравносмещенная передача – может быть составлена: а) из двух положительных колес с разными коэффициентами смещения (χ1 ≠ χ2); б) из положительного и отрицательного колес с разными по модулю коэффициентами смещения (χ1 ≠ -χ2); в) из двух отрицательных колес с разными коэффициентами смещения (-χ1 ≠ -χ2). На практике чаще применяется передача с положительными колесами. При такой передаче действительный угол зацепления больше стандартного αW > α, толщина зубьев шестерни и колеса больше, чем ширина впадины (S1,2 > e1,2) и сумма их получается больше шага (S1+S2>P). Так как данная передача не вписывается в заданные межосевое расстояние и шаг, то оси зубчатых колес необходимо раздвигать, применяя коэффициент уравнительного смещения Δу. За оптимальный угол зацепления принимается угол aW = 27о.
Таблица 4.2 - Формулы для определения размеров корригированных
зубчатых колес по относительным сдвигам рейки
| Что требуется найти | Вид зацепления | ||
| Наименование | Обозначение | Неравносмещенное | Равносмещенное |
| Шаг по делитель- ной окружности | Р | Р = πm | Р = πm |
| Радиус делитель- ной окружности | R1 | R1=mz1/2 | R1=mz1/2 |
| R2 | R2=mz2/2 | R2=mz2/2 | |
| Толщина зуба по делительной окружности | S1 | S1=m(π/2+2χ1tgα) | S1=m(π/2+2χ1tgα) |
| S2 | S2=m(π/2+2χ2tgα) | S2=m(π/2+2χ2tgα) | |
| Радиус основной окружности | Rb1 | Rb1=R1cosα | Rb1=R1cosα |
| Rb2 | Rb2=R2cosα | Rb2=R2cosα | |
| Радиус окружности впадин | Rf1 | Rf1=R1-m(1,25-χ1) | Rf1=R1-m(1,25-χ1) |
| Rf2 | Rf2=R2-m(1,25-χ2) | Rf2=R2-m(1,25-χ2) | |
| Межосевое расстояние | аW | аW=m[(z1+z2)/2+y] | аW=m[(z1+z2)/2+y] |
| Радиус начальной окружности | RW1 | RW1=R1[1+2y/(z1+z2)] | RW1=R1 |
| RW2 | RW2=R2[1+2y/(z1+z2)] | RW2=R2 | |
| Глубина захода зубьев | hЗ | hЗ=(2-Δу)m | hЗ=2m |
| Высота зуба | h | h =hЗ+0,25m | h =hЗ+0,25m |
| Радиус окружности выступов | Ra1 | Ra1=R1+m 1+ χ1- Δу) | Ra1=R1+m (1+ χ1) |
| Ra2 | Ra2=R2+m(1+ χ2- Δу) | Ra2=R2+m (1+ χ2) | |
| Коэффициент воспринимаемого смещения | у | у = χ1+ χ2 - Δу | у = 0 |
| Примечание. Все размеры в мм. Угол зацепления α = 200. |
Примечание. Коэффициенты смещения χ1, χ2 для неравносмещенного зацепления выбрать по приложениям 2, 3, 4 приложения; для равносмещенного зацепления выбрать по приложению 5. Коэффициент уравнительного смещения Δу выбрать по приложениям 1, 2. Изображение неравносмещенного зацепления представлено на рисунке 4.27.
Мы рассмотрели основные законы внешнего эвольвентного зацепления, которые верны и для других видов зацепления. О них мы расскажем коротко.
Вопросы для самоконтороля
1. Какая передача более компактная: цилиндрическая, коническая или червячная?
2. Сформулируете основной закон зацепления.
3. Запишите передаточное отношение одно и многоступенчатого редукторов.
4. Что такое модуль и шаг зубчатого зацепления?
5. При каких условиях возникает явление подрезания. Какие элементы зуба подрезаются: ножка или головка?
6. Для каких целей производят смещение режущего инструмента?
7. В чем отличие метода обкатки от метода копирования?
Дата добавления: 2015-10-19; просмотров: 1550;
