Обработка результатов экспертных оценок совокупности объектов, заключенных в одном вопросе
Одним из примеров экспертного опроса для случая совокупности (перечня) объектов, оцениваемых в рамках одного вопроса, является экспертный опрос по оценке относительной важности объектов, направлений или вариантов развития в целях установления последовательности проведения различных работ (НИР, ОКР и т.д.), очередности финансирования, распределения ресурсов и решения других вопросов.
Основной процедурой обработки результатов данного экспертного опроса является ранжирование объектов или направлений исходной совокупности по их относительной важности.
Ранжирование представляет собой процесс расположения направлений (целей, задач, вариантов, объектов, явлений, факторов) в порядке убывания или возрастания какого-либо характерного свойства или характеристики.
Экспертам, участвующим в данном опросе, предлагается заранее разработанный перечень с просьбой оценить относительную важность его элементов. Относительная важность направления развития, исследований или разработок может оцениваться экспертами путем назначения некоторых количественных оценок по принятой шкале, например по 100-балльной.
Полученные оценки представляются в форме таблицы, строки которой соответствуют экспертам (i - индекс эксперта, ), а столбцы - оцениваемым элементам перечня (j - индекс элементов перечня, ). В таблице, приведенной ниже, Cij - балл относительной важности, присвоенный i-м экспертом (i=1…n) j-му элементу перечня (j=1…m).
| Эксперт | Объект | ||||||
| … | j | … | m | ||||
| C11 | C12 | C13 | … | C1j | … | C1m | |
| C21 | C22 | C23 | … | C2j | … | C2m | |
| C31 | C32 | C33 | … | C3j | … | C3m | |
| … | … | … | … | … | … | … | … |
| i | Ci1 | Ci2 | Ci3 | … | Cij | … | Cim |
| … | … | … | … | … | … | … | … |
| n | Cn1 | Cn2 | Cn3 | … | Cnj | … | Cnm |
При обработке результатов экспертных оценок относительной важности используют следующие показатели обобщенного мнения:
1. Среднее арифметическое значение оценок j -го направления исследований (элемента) в баллах:
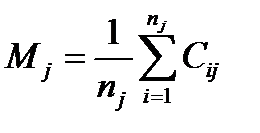
определяется для каждого из m элементов перечня и может принимать в данном случае значения в пределах от 0 до 100 баллов. Чем больше значение Mj , тем больше, по мнению экспертов, важность j -го элемента.
2. Частота максимально возможных оценок (100 баллов), полученных j-м элементом:
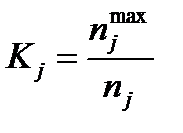
где njmax - число экспертов из оценивавших j-й элемент и давших ему максимальную оценку (100 баллов);
nj - общее число экспертов, принявших участие в оценке j-го элемента.
Коэффициент Kj определяют для каждого из m элементов перечня, он может принимать значения в пределах от 0 до 1. Важность j-го элемента возрастает при изменении от 0 до 1. Частота максимально-возможных оценок характеризует важность j-го элемента с точки зрения количества присужденных ему «первых мест».
3. Коэффициент удельного веса K уд j оценок j-го элемента:
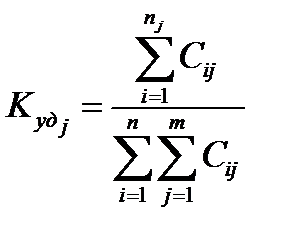 Здесь в числителе формулы стоит сумма баллов, присвоенных j-му элементу всеми экспертами; в знаменателе - общая сумма баллов, присвоенных экспертами всем элементам перечня.
Здесь в числителе формулы стоит сумма баллов, присвоенных j-му элементу всеми экспертами; в знаменателе - общая сумма баллов, присвоенных экспертами всем элементам перечня.
Коэффициент. определяется для каждого из m элементов. Сумма по всем элементам равна 1. Показатель также следует рассматривать как показатель важности j-го элемента. Чем выше значение, тем большую важность имеет данный элемент.
4. Коэффициент активности экспертов Kэj для j-го элемента:

Чем больше этот коэффициент, тем больше экспертов считают себя компетентными в оценке j-го элемента перечня.
5. Сумма рангов , полученных j-м элементом.
Для определения рангов проводится ранжирование оценок относительной важности , данных каждым экспертом по всем элементам. Для этого оценки Cij обозначают числами натурального ряда таким образом, что ранг 1 присваивается максимальной оценке, ранг 2 - второй по величине и т.д. Если все m, оценок различны, то соответствующие числа натурального ряда есть ранги оценок соответствующего эксперта. Если среди оценок , данных определенным экспертом, есть одинаковые, то этим оценкам присваивается одинаковый ранг, равный среднему арифметическому соответствующих соседних чисел натурального ряда.
Очевидно, что при сравнении важности элементов по наиболее важными следует считать направления, характеризующиеся наименьшим значением суммы рангов.
Наряду с показателями обобщенного мнения весьма существенным является определение показателей степени согласованности мнений экспертов. К этим показателям относятся:
1. Дисперсия оценок , данных j-му элементу перечня:
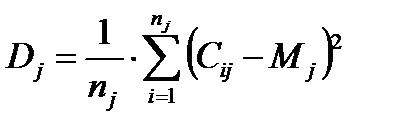
2. Среднеквадратическое отклонение оценок , полученных j-м элементом:
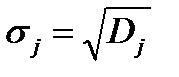
3. Коэффициент вариации оценок , полученных j-м элементом:
Коэффициент вариации характеризует степень согласованности мнений экспертов об относительной важности j-го элемента. Чем больше значение , тем выше степень согласованности мнений экспертов.
4. Коэффициент парной ранговой корреляции между оценками двух любых экспертов α и β,
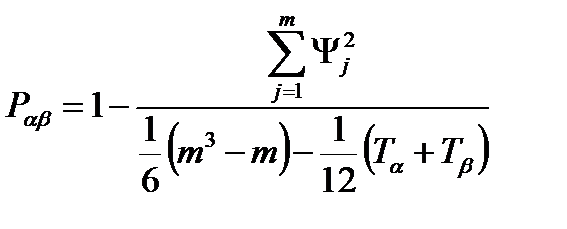 где Ψj - разность (по модулю) величин рангов оценок j-го элемента, присвоенных экспертами α и β,
где Ψj - разность (по модулю) величин рангов оценок j-го элемента, присвоенных экспертами α и β,
 Tα и Tβ - показатели связанных рангов оценок экспертов α и β.
Tα и Tβ - показатели связанных рангов оценок экспертов α и β.
Коэффициент парной ранговой корреляции дает представление о степени согласованности мнений и может принимать значения. Значение соответствует полному совпадению оценок в рангах двух экспертов. Значение соответствует двум взаимно противоположным ранжировкам важности элементов.
5. Коэффициент конкордации W является показателем степени согласованности мнений экспертов об относительной важности всех предложенных для оценки элементов. Определение W осуществляется следующим образом:
А) определяется среднее арифметическое сумм рангов оценок, полученных всеми элементами:
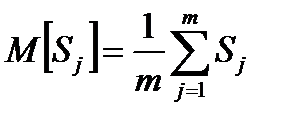
Б) вычисляются отклонения суммы рангов оценок, полученных j-м элементом, от среднего арифметического сумм рангов оценок, полученных всеми элементами:

В) определяются показатели Ti - связанных (равных) рангов оценок, назначенных i-м экспертом. Если все m рангов оценок, назначенных i-м экспертом, различны, то Ti=0 ; если среди рангов оценок есть одинаковые, то
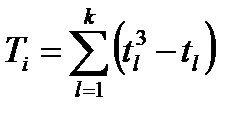
где l - индекс группы равных рангов (l=1…k);
tl- количество равных рангов в l-й группе;
Г) определяется коэффициент конкордации
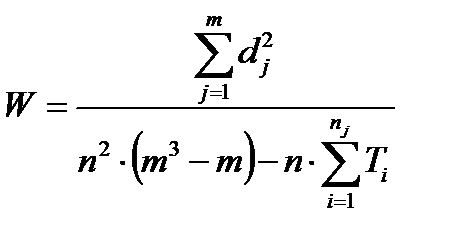
Коэффициент конкордации может принимать значения в пределах от 0 до 1 при полной согласованности мнений экспертов . Изменение от 0 до 1 соответствует увеличению степени согласованности их мнений.
Небольшое значение коэффициента конкордации свидетельствует о слабой согласованности мнений экспертов и является обычно следствием таких причин:
1) в рассматриваемой совокупности экспертов действительно отсутствует общность мнений;
2) внутри рассматриваемой группы экспертов существуют подгруппы с высокой согласованностью мнений, однако обобщенные мнения таких подгрупп противоположны.
Для выявления подгрупп экспертов, внутри которых согласованность мнений высока, целесообразен следующий подход. Осуществляется перебор с последовательным исключением экспертов. Одного эксперта исключают из совокупности и подсчитывают коэффициент конкордации для оставшихся экспертов. Если значение оказалось больше, чем значение для полной совокупности экспертов, то данный эксперт исключается из группы. Подобные расчеты проводятся последовательно для каждого эксперта. В результате может быть отобрана группа с высокой степенью согласованности мнений экспертов.
Если коэффициент конкордации достаточно высок, то необходимо убедиться в том, что его значение не случайно. Для этого оценивают репрезентативность экспертных заключений, основываясь на общих принципах оценки статистических нулевых гипотез.
В качестве критерия в данном случае принимается критерий Пирсона χ2, вычисляемый по результатам статистических наблюдений.
Проверку статистической значимости целесообразно проводить следующим образом. Для критерия χ2 задаемся некоторым уровнем значимости α (чаще 0,05). Чем ниже уровень значимости, тем больше вероятность P того, что согласованность мнений выбранной группы экспертов не случайна (P=1-α).
Уровень значимости, превышающий значение 0,05, будем считать показателем случайной согласованности экспертов.
Критерий Пирсона определяется по формуле
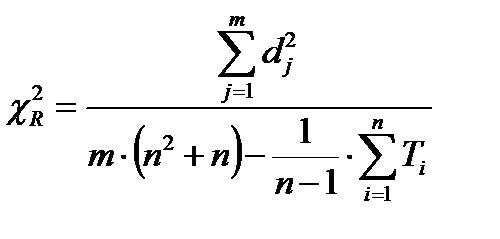
В таблице значений χ2 для данного числа степеней свободы k=n-1 находится соответствующее табличное значение уровня значимости α*. Найденное значение сравнивается с выбранным значением уровня значимости .
Если α >α*, то с вероятностью Р=1 - α = 0,95 значение не случайно.
Дата добавления: 2015-10-19; просмотров: 1638;
