Методический инструментарий оценки уровня риска

Уровень финансового риска – это главный показатель оценки уровня финансовой безопасности предприятия, который характеризует степень защиты финансовой деятельности предприятия от угроз внешнего и внутреннего характера.

Методический инструментарий оценки уровня риска:

1. Методический инструментарий количественной оценки уровня финансового риска:

а) экономико-статистические методы:

- уровень финансового риска:

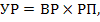
где УР – уровень финансового риска;

ВР – вероятность возникновения данного финансового риска;

РП – размер возможных финансовых потерь при реализации данного риска.

- дисперсия:

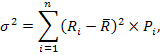
где 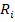– конкретное значение возможных вариантов ожидаемого дохода по рассматриваемой финансовой операции;

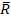– среднее ожидаемое значение дохода по рассматриваемой финансовой операции;

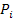– возможная частота получения отдельных вариантов ожидаемого дохода по финансовой операции;

n – число наблюдений.

- среднеквадратической (стандартное) отклонение:

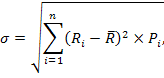
Пример с.127

Пример: Необходимо оценишь уровень финансового риска по инвестиционной операции по следующим данным: на рассмотрение представлено два альтернативных инвестиционных проекта (проект "А ” и проект иБ ”)с вероятностью ожидаемых доходов, представленной в табл. 4,1

Таблице 4.1 Распределение вероятности ожидаемых доходов по двум инвестиционным проектам

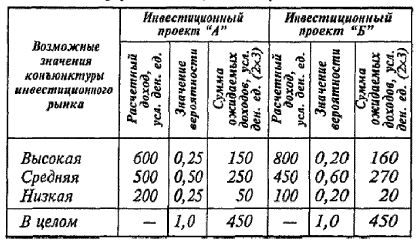
Сравнивая данные но отдельным инвестиционным проектам, можно увидеть, что расчетные величины доходов по проекту "А ” колеблются в пределах от 200 до 600 усл. ден. ед. при сумме ожидаемых доходов в целом 450уел. ден. ед. По проекту «Б» сумма ожидаемых доходов в целом также составляет 450 уел. ден. ед., однако их колеблемость осуществляется в диапазоне от 100' до 800 уел. ден. ед. Даже такое простое сопоставление позволяет сделать вывод о там, что риск реализации инвестиционного проекта «А» значительно меньше, чем проекта “Б”, где колеблемость расчетного дохода выше. Более наглядное представление об уровне риска дают результаты расчета среднеквадратического (стандартного) отклонения, представленные в табл. 4.2.

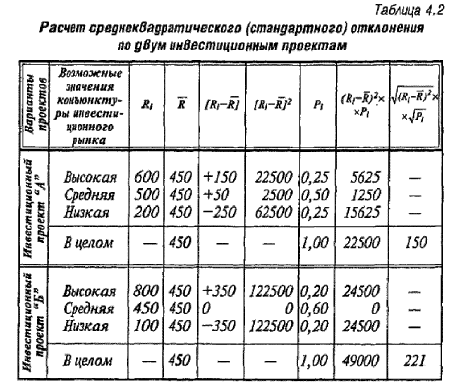
Результаты расчета показывают, что среднеквадратическое (стандартное) отклонение по инвестиционному проекту “А ” составляет 156, в то время как по инвестиционному проекту "Б“ — 221, что свидетельствует о большем уровне его риска.

- коэффициент вариации:

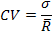
Пример с.130

Пример: Необходимо рассчитать коэффициент вариации по трем инвестиционным проектам при различных значениях среднеквадратического (стандартного) отклонения и среднего ожидаемого значения доходе по ним. Исходные данные и результаты расчета приведены в табл. 4.3.

Результаты расчета показывают, что наименьшее значение коэффициента вариации — по проекту "А ”, а наибольшее — по проекту "В ”. Таким образом, хотя ожидаемый доход по проекту "В” на 33% выше, чем по проекту “А ” 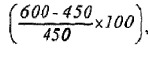уровень риска по нему, определяемый коэффициентом вариации, выше 61 %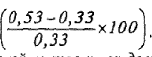

Следовательно, при сравнении уровней рисков по отдельным инвестиционным проектам предпочтение при прочих равных условиях следует отдавать тому из них, по которому

значение коэффициентов вариации самое низкое (что свидетельствует о на и лучшем соотношении доходности и риска).

- бета коэффициент:

где К – степень корреляции между уровнем доходности по индивидуальному виду ценных бумаг или по их портфелю и средним уровнем доходности данной группы фондовых инструментов по рынку в целом;

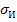– среднеквадратическое (стандартное) отклонение доходности по индивидуальному виду ценных бумаг ( по их портфелю в целом);

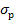– среднеквадратическое отклонение доходности по фондовому рынку в целом.

б) экспертные методы оценки уровня финансового риска.

в) аналоговые методы оценки уровня финансового риска.

2. Методический инструментарий формирования необходимого уровня доходности финансовых операций с учетом уровня риска:

а) определение необходимого уровня премии за риск:

где 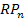– уровень премии за риск по конкретному финансовому (фондовому) инструменту;

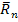– средняя норма доходности на финансовом рынке;

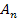– безрисковая норма доходности на финансовом рынке;

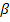– бета-коэффициент.

Пример с.132

Пример: Необходимо рассчитать уровень премии за риск по трем видом акций. Исходные данные и результаты расчета приведены в табл. 4.4.

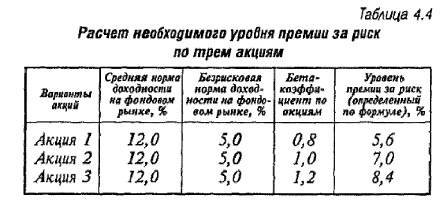
Результаты расчета показывают, что уровень премии за риск возрастает пропорционально росту бета - коэффициента, т.е. уровня систематического риска.

б) Сумма премии за риск:

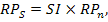
где 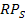– сумма премии за риск по конкретному финансовому (фондовому) инструменту в настоящей стоимости;

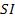– стоимость (котируемая цена) конкретного финансового (фондового) инструмента;

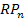– уровень премии за риск по конкретному финансовому (фондовому) инструменту.

Пример с.133

Пример: Исходя из котируемой цены трех акций на фондовом рынке и результатов расчета уровня премии за риск по ним (см, предыдущий пример) определить сумму этой премии по каждой акции.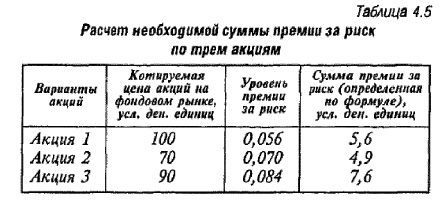

в) Общий (необходимый) уровень доходности финансовых операций с учетом фактора риска:

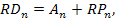
где 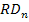– общий уровень доходности по конкретному финансовому (фондовому) инструменту с учетом фактора риска;

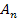– безрисковая норма доходности на финансовом рынке;

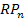– уровень премии за риск по конкретному финансовому (фондовому) инструменту.

При определении уровня избыточной доходности (премии за риск) всего портфеля ценных бумаг на единицу его риска используется «коэффициент Шарпа»:

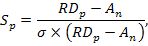
где 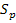– коэффициент Шарпа, измеряющий избыточную доходность портфеля на единицу риска, характеризуемую среднеквадратическим (стандартным) отклонением этой избыточной доходности;

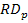– общий уровень доходности портфеля;

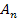– уровень доходности по безрисковому финансовому инструменту инвестирования;

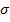– среднеквадратическое отклонение избыточной доходности.

Пример с.134

Пример: Следует рассчитать необходимый общий уровень доходности по трем видам акций. Исходные данные и результаты расчета приведены в табл. 4.6.

4.2 Методический инструментарий оценки «стоимости под риском» (VAR)

«Стоимость под риском» (VAR) представляет собой показатель статистической оценки выраженного в денежной форме максимально возможного размера финансовых потерь при установленном виде распределения вероятности факторов, влияющих на стоимость активов (инструментов), а также заданном уровне вероятности возникновения этих потерь на протяжении расчетного периода времени.

Основу методологии расчета показателя «стоимость под риском» составляют три основных элемента:

- установленный риск-менеджером вид распределения вероятностей рисковых факторов: нормальное распределение, распределение Лапласа, Стьюдента и т.д.;

- задаваемый риск-менеджером уровень вероятности того, что максимально возможный размер финансовых потерь не превысит расчетное значение этого показателя (доверительный уровень);

- устанавливаемый риск-менеджером расчетный период времени его оценки (период поддержания позиции).

Методический инструментарий оценки «стоимость под риском»:

1. Аналитический (или параметрический) метод.

2. Метод исторического моделирования (или моделирования по историческим данным).

3. Метод имитационного моделирования ( метод Монте-Карло).

4. Метод анализа сценариев.

5. Метод дерева вероятностей.