Принцип перестановочной двойственности
Предположим, что известен электромагнитный процесс, описываемый следующими уравнениями Максвелла:
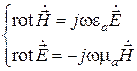 ю
ю
Обращает на себя внимание симметрия этих двух уравнений. Действительно, уравнения переходят одно в другое при замене вида
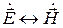 ,
, 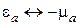 .
.
Последние соотношения являются математическим выражением принципа перестановочной двойственности для электромагнитного поля, обоснованного впервые А. А. Пистолькорсом в 1944 г.
Физическое содержание этого принципа заключается в следующем. Если известно полное решение какой-либо электромагнитной задачи, то простая перестановка позволяет автоматически получить решение двойственной (дуальной) задачи, в которой конфигурация линий электрического поля повторяет аналогичную конфигурацию линий магнитного поля в исходном электромагнитном процессе и наоборот. При этом, поскольку в результате перестановки уравнения Максвелла не меняют своего вида, двойственный электромагнитный процесс действительно существует.
Естественно считать, что исходное электромагнитное поле возбуждается сторонними электрическими токами. В этом случае можно полагать, что двойственный процесс возбуждается сторонними магнитными токами, как это было показано в предыдущем разделе. Однако для сохранения симметрии уравнений Максвелла плотность стороннего магнитного тока должна быть введена во второе уравнение с обратным знаком. Таким образом, получаем систему уравнений Максвелла с учетом сторонних магнитных токов:
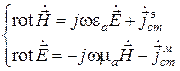 .
.
Дополнительное перестановочное соотношение для плотностей сторонник токов приобретает вид
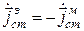 .
.
Дата добавления: 2015-10-19; просмотров: 2719;
