Критическая длина волны

Выясним условия существования тех или иных типов волн в зависимости от их индекса, ширины волновода 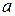и длины волны генератора 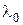. При этом будем исходить из сформулированного выше условия, которое на основании формул для суммарного поля между двумя плоскостями

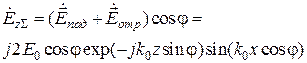
и

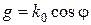
принимает вид

,

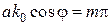где 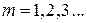− индекс типа волны.

Действительно, при выполнении этого условия амплитудная синусоидальная функция, описывающая распределение поля в поперечном сечении волновода, обращается в нуль на верхней и нижней стенках (рисунок 14).

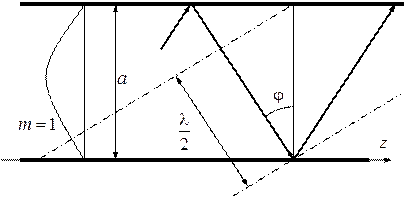
Рисунок 14 − Распространение волны в двухплоскостном волноводе

Это условие может быть переписано в следующем эквивалентном виде:

.

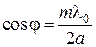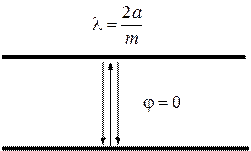
Рисунок 15 − Распространение при разной длине волны

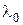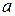Отсюда можно сделать вывод: при фиксированных параметрах и каждому индексу 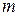соответствует определенное значение угла падения 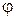, обеспечивающеее условие существования волн типов 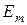или 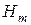(рисунок 15). Отметим при этом, что с ростом индекса угол падения должен уменьшаться.

Поскольку левая часть последнего соотношения ограничена в интервале 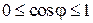, данное соотношение не может быть выполнено при любых 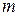, 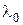и 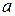. Действительно, для любого индекса 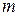найдется такая длина волны генератора, которую будем называть критической длиной волны данного типа и обозначать , для которой выполнение условий возможно лишь при максимальном значении 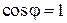, т.е.

.

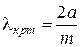Если теперь выбрать значение 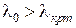, то граничные условия на стенках волновода не могут быть выполнены ни при каком вещественном значении угла падения. Физически это означает невозможность существования колебания данного типа в виде бегущей волны. Явления, происходящие в волноводе на критической длине волны, могут быть сформулированы следующим образом. Поскольку 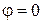, образуется стоячий волновой процесс в поперечной плоскости, т.е. никакого волнового движения, а следовательно, и передачи энергии вдоль оси 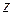не происходит. Однако важно подчеркнуть, что на критической длине волны

, .

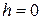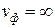Теперь можно сформулировать основной вывод из приведенных рассуждений. Каждый тип колебаний с индексом 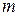может существовать как бегущая волна в области длин волн, удовлетворяющих равенству

.

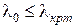Волны, более длинные, чем , по волноводу на данном типе колебаний распространяться не могут. Принято говорить, что область частот, удовлетворяющая неравенству 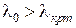, является областью отсечки данного типа колебаний.

Тип волны, обладающий наибольшей критической длиной, носит название основного (или низшего) в данном волноводе. Для рассматриваемого здесь двухплоскостного волновода низших типов волн два: это типы 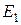и 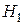, для них 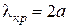. Итак, если длина волны генератора превосходит удвоенную ширину волновода, то никакие волны Е- и Н-типов распространяться в нем не могут. Если 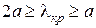, то в волноводе могут существовать лишь волны низших типов. При 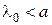появляется возможность возникновения двух волн высших типов 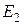, 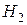и т.д.

Знание критической длины волны позволяет для конкретной длины волны генератора определить фазовую скорость на любом типе колебаний:

.

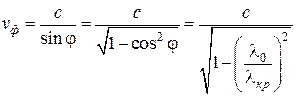Аналогично находится длина волны в волноводе:

.

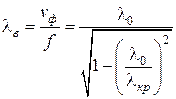Формулы подобного вида будут часто встречаться в дальнейшем, при рассмотрении волноводов разного типа.