Фазовая скорость направляемых волн

Приведенные на рисунке 10 и рисунке 11 картины силовых линий для волн типов Е и H, являются, по существу, мгновенными фотографиями поля, отображающими волновые процессы в какой-либо фиксирванный момент времени. Несомненно, что эти картины перемещаются в пространстве с некоторой скоростью, которую нужно вычислить.

Для определенности будем рассматривать волну типа Е, поскольку для волн типа Н выводы будут полностью аналогичными. Запишем комплексные амплитуды электрических векторов падающей и отраженной волн в следующем виде:

,

где − фазовая постоянная распространения, или волновое число вакуума.

Вектор суммарного поля будет обладать составляющими, равными суммам составляющих векторов 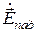и 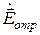. В частности, суммарная 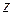-я составляющая оказывается равной

.

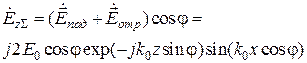Первый сомножитель в этой формуле является несущественной произвольной постоянной. Поэтому проанализируем второй и третий сомножители, описывающие зависимость составляющей 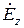от декартовых координат.

Наличие второго сомножителя 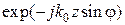показывает, что результирующее поле представляет собой волну, бегущую вдоль координаты 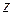, причем постоянная распространения зависит от угла падения. В дальнейшем будем называть эту постоянную распространения продольным волновым числом и обозначать через :

.

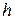Наличие третьего сомножителя в формуле для суммарного поля приводит к тому, что рассматриваемый волновой процесс существенно отличается от однородной плоской волны, поскольку здесь амплитуда поля уже не постоянна в пределах волнового фронта, параллельного плоскости , а изменяется по синусоидальному закону вдоль поперечной координаты 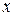. Легко видеть, что скорость изменения амплитуды определяется «поперечной частотой»

,

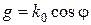которую бдуем называть поперечным волновым числом. Продольное и поперечное волновые числа связаны очевидным соотношением (рисунок 12)

.

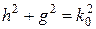Рисунок 12 − Волновые числа и фазовая скорость

Физическая сущность поперечного и продольного волновых чисел остается той же, что и для полного волнового числа: они показывают расстояние, которое должна пройти волна в метрах, чтобы ее фаза изменилась на , т.е. на полный период. Для продольного волнового числа это расстояние по оси 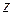, для поперечного − по оси .

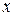Итак, определено важное свойство направляемых волн, состоящее в следующем. Данный волновой процесс является неоднородной плоской волной, которая распространяется вдоль оси 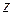. При этом амплитуда поля изменяется вдоль поперечной координаты 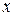по закону стоячей волны.

Вычислим скорость перемещения поверхности равных фаз (волнового фронта) вдоль координаты 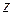, т.е. фазовую скорость направляемой волны. Поскольку здесь роль постоянной распространения играет продольное волновое число 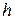, то из общего выражения для фазовой скорости будем иметь:

.

Отсюда следует принципиально важный вывод: за исключением предельного случая фазовая скорость направляемых волн всегда превосходит скорость плоских электрмагнитных волн, в частности, скорость света в вакууме: . Данный вывод нуждается в обсуждении, поскольку, согласно теории относительности, скорость света в вакууме имеет предельный характер. Однако следует учитывать, что это утверждение относится лишь к движению материальных объектов. В противоположность этому фазовая скорость является скоростью перемещения в пространстве некоторой воображаемой поверхности − волнового фронта. Поэтому ограничения, накладываемые теорией относительности, в данном случае не справедливы.

Неограниченное возрастание фазовой скорости при стремлении к нулю угла падения можно проиллюстрировать следующим образом. Пусть фазовые фронты падающей волны движутся в пространстве со скоростью 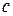так, как это показано на рисунке 12. Можно найти скорость скорость перемещения точки пересечения фазового фронта с направляющей поверхностью. Если за единицу времени фронт падающей волны проходит расстояние , то точка его пересечения с осью 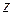должна пройти расстояние . Так как 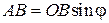, то 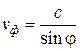, на что и указывает приведенная выше формула. В предельном случае падения волны по направлению нормали фазовая скорость вдоль оси 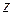обращается в бесконечность.