Падение плоской волны с параллельной поляризацией

Будем полагать, что на идеально проводящую поверхность под некоторым углом 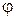падает монохроматическая волна. Предположим также, что верхнее полупространство представляет собой вакуум, т.е. однородную среду с проницаемостями 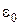, 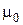. На рисунке изображены мгновенные положения последовательности волновых фронтов падающей волны, отстоящих друг от друга на половину длины волны. Ясно, что фазы поля в них отличаются при этом на 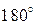. 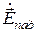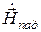Взаимная ориентация векторов и , обозначенная на волновых фронтах, соответствует принятому направлению вектора Пойнтинга .

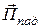Известно, что граничные условия на поверхности идеального проводника заключаются в равенстве нулю тангенциальной составляющей электрического вектора на границе раздела. Выполнение данного условия возможно лишь при наличии отраженной волны.

Рисунок 9 − Падение плоской электромагнитной волны с параллельной поляризацией на идеально проводящую плоскость

На рисунке 9 построена система поверхностей равных фаз для отраженной волны, векторы поля которой обладают следующими свойствами:

1. Амплитуды и совпадают с амплитудам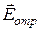и и 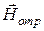соответственно: 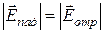и 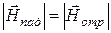, поскольку потери в идеальном проводнике отсутсвуют и модуль коэффициента отражения равен единице при любом угле падения.

2. Направление 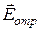согласовано с направлением таким образом, что на границе раздела тангенциальная составляющая суммарного электрического вектора 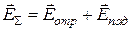равна нулю.

3. Взаимная ориентация векторов 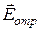и 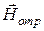обусловлена указанным на рисунке направлением вектора Пойнтинга 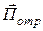, который перпендикулярен поверхности равных фаз отраженной волны.

Проведем теперь векторное сложение полей падающей и отраженной волны в узлах образующейся сетки волновых поверхностей. Результат его представлен на рисунке, причем могут быть сделаны следующие выводы:

1. Силовые линии суммарного магнитного поля имеют вид бесконечных нитей, направленных параллельно оси 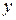; в некоторых узлах сетки магнитное поле полностью компенсируется.

2. Векторы 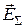лежат в плоскости , причем ориентация этих векторов меняется непрерывно от точки к точке.

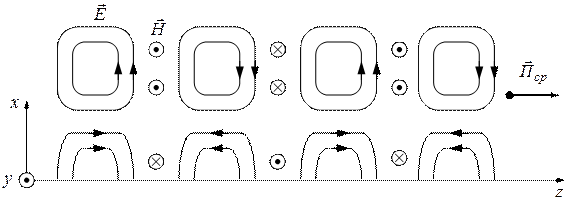
Рисунок 10 − Результирующая картина силовых линий поля при падении плоской волны с параллельной поляризацией

Полученная картина векторной интерференции позволяет построить эскиз силовых линий результирующего волнового процесса. Для этого, например, силовые линии поля 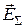должны быть построены так, чтобы результирующие векторы в узлах сетки были бы к ним касательны.

Следует принять во внимание, что рассматривались лишь те волновые фронты, в пределах которых мгновенные значения векторов поля максимальны. Если произвести более детальное построение, включив в рассмотрение волновые фронты с промежуточными значениями фазы, то получим окончательную картину силовых линий, изображенную на рисунке. Здесь графически показано постепенное изменение напряженностей поля в пространстве.