Связь между продольными и поперечными составляющими поля
Результаты, полученные ранее, носят скорее качественно-геометрический характер. В данном разделе будет развит метод анализа направляемых волн, основанный на решении уравнений Максвелла, и пригодный для весьма обширного класса волноводных структур. Основным здесь является то, что анализируемая направляемая волна представляет собой неоднородную плоскую волну, т.е. ее амплитуда вдоль волнового фронта не является постоянной. В случае, если за ось распространения выбрана ось 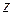 , комплексная амплитуда любой составляющей электромагнитного поля может быть записана в виде
, комплексная амплитуда любой составляющей электромагнитного поля может быть записана в виде
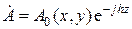 .
.
Этот, вообще говоря, довольно частный вид зависимости поля от пространственных координат позволяет весьма просто выразить производные от поля по 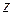 :
:
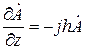 ,
, 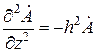 , и т.д.
, и т.д.
Пусть электромагнитный процесс в области, свободной от источников, описывается уравнениями Максвелла
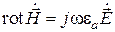 ,
, 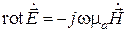 .
.
В развернутой форме будем иметь
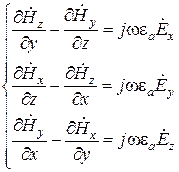 ,
,
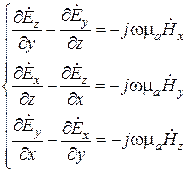
Если теперь выразить производные по 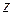 в соответствии с принятым видом комплексной амплитуды поля
в соответствии с принятым видом комплексной амплитуды поля 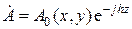 , то эти системы упростятся:
, то эти системы упростятся:
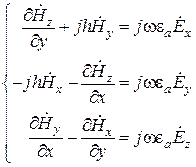 ,
,
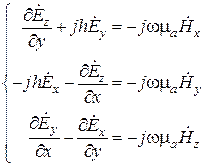 .
.
Здесь принципиально важно то, что в соответствии с этими системами поперечные составляющие 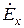 и
и 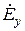 ,
, 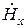 и
и 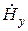 представлены в виде линейных кобминаций из производных продольных составляющих
представлены в виде линейных кобминаций из производных продольных составляющих 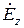 и
и 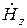 по поперечным координатам
по поперечным координатам 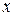 ,
, 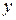 . Действительно, рассматривая, например, совместно первое уравнение из первой системы и второе уравнение из второй системы, получаем систему линейных алгебраических уравнений относительно
. Действительно, рассматривая, например, совместно первое уравнение из первой системы и второе уравнение из второй системы, получаем систему линейных алгебраических уравнений относительно 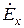 и
и 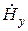 , причем в правой части этотй системы окажутся производные
, причем в правой части этотй системы окажутся производные 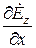 и
и 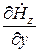 . Решая подобные системы уравнений, приходим к следующему результату:
. Решая подобные системы уравнений, приходим к следующему результату:
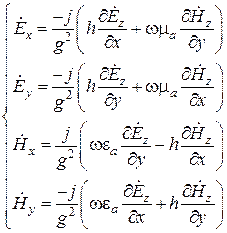 .
.
Здесь 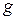 − поперечное волновое число данного процесса,
− поперечное волновое число данного процесса, 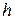 − продольное волновое число, связанные следующим образом:
− продольное волновое число, связанные следующим образом:
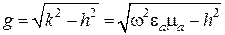 .
.
Приведенная система может рассматриваться как формулы перехода между продольными и поперечными составляющими направляемого электромагнитного процесса. Важность их состоит в том, что теперь задача сведена к нахождению лишь двух функций 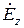 и
и 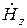 , остальные составляющие определяются через них путем дифференцирования. Это еще раз подчеркивает принципиальное значение составляющих
, остальные составляющие определяются через них путем дифференцирования. Это еще раз подчеркивает принципиальное значение составляющих 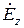 и
и 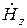 , по наличию или отсутствию которых можно условно проводить классификацию направляемых волн. Фактически это решение даже несколько проще, поскольку для волн Е-типа отсутствует продольная составляющая магнитного поля
, по наличию или отсутствию которых можно условно проводить классификацию направляемых волн. Фактически это решение даже несколько проще, поскольку для волн Е-типа отсутствует продольная составляющая магнитного поля 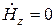 , а для волн Н-типа будем иметь
, а для волн Н-типа будем иметь 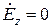 .
.
Дата добавления: 2015-10-19; просмотров: 1091;
