Дифференциальные уравнения теплопроводности
Решение задач по определению температурного поля осуществляется на основании дифференциального уравнения теплопроводности, выводы которого показаны в специальной литературе. В данном пособии приводятся варианты дифференциальных уравнений без выводов.
При решении задач теплопроводности в движущихся жидкостях, характеризующих нестационарное трехмерное температурное поле с внутренними источниками теплоты, используется уравнение
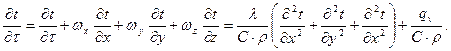 (4.10)
(4.10)
Уравнение (4.10) является дифференциальным уравнением энергии в декартовой системе координат (уравнение Фурье ¾ Кирхгофа). В таком виде оно применяется при изучении процесса теплопроводности в любых телах.
Если wx=wy=wz=0, т. е. рассматривается твердое тело, и при отсутствии внутренних источников теплоты qv=0, тогда уравнение энергии (4.10) переходит в уравнение теплопроводности для твердых тел (уравнение Фурье)
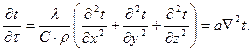 (4.11)
(4.11)
Величину l/С×r=a, м2/сек в уравнении (4.10) называют коэффициентом температуропроводности, который является физическим параметром вещества, характеризующим скорость изменения температуры в теле при неустановившихся процессах.
Если коэффициент теплопроводности характеризует способность тел проводить теплоту, то коэффициент температуропроводности является мерой теплоинерционных свойств тела. Из уравнения (4.10) следует, что изменение температуры во времени ¶t/¶t для любой точки пространства пропорционально величине «а», т. е. скорость изменения температуры в любой точке тела будет тем больше, чем больше коэффициент температу-ропроводности. Поэтому при прочих равных условиях выравнивание температур во всех точках пространства будет происходить быстрее в том теле, которое обладает большим коэффициентом температуропроводности. Коэффициент температуропроводности зависит от природы вещества. Например, жидкости и газы обладают большой тепловой инерционностью и, следовательно, малым коэффициентом температуропроводности. Металлы обладают малой тепловой инерционностью, так как они имеют большой коэффициент температуропроводности.
Для обозначения суммы вторых производных по координатам в уравнениях (4.10) и (4.11) можно использовать символ Ñ2, так называемый оператор Лапласа, и тогда в декартовой системе координат
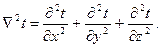
Выражение Ñ2t в цилиндрической системе координат имеет вид
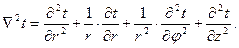
Для твердого тела в стационарных условиях с внутренним источником теплоты уравнение (4.10) преобразуется в уравнение Пуассона
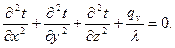 (4.12)
(4.12)
Наконец, для стационарной теплопроводности и при отсутствии внутренних источников теплоты уравнение (4.10) принимает вид уравнения Лапласа
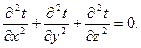 (4.13)
(4.13)
Дифференциальное уравнение теплопроводности в цилиндрических координатах с внутренним источником теплоты
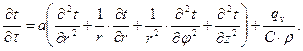 (4.14)
(4.14)
Дата добавления: 2015-10-13; просмотров: 1939;
