Условия однозначности для процессов теплопроводности

Так как дифференциальное уравнение теплопроводности выведено на основе общих законов физики, то оно характеризует явление теплопроводности в самом общем виде. Поэтому можно сказать, что полученное дифференциальное уравнение характеризует целый класс явлений теплопроводности. Чтобы из бесчисленного количества выделить конкретно рассматриваемый процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми, которые включают в себя:

а) геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;

б) физические условия, характеризующие физические свойства среды и тела (l, С_z, r, а и др.);

в) временные (начальные) условия, характеризующие распределение температур в изучаемом теле в начальный момент времени;

г) граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.

Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано следующим образом при t=0:

t = ¦₁(x, y, z). (4.15)

В случае равномерного распределения температуры в теле начальное условие упрощается: при t=0; t=t₀=idem.

Граничные условия могут быть заданы несколькими способами.

А. Граничные условия первого рода, задающие распределение температуры на поверхности тела t_c для каждого момента времени:

t_c = ¦₂(x, y, z, t). (4.16)

В частном случае, когда температура на поверхности является постоянной на протяжении всего времени протекания процессов теплообмена, уравнение (4.16) упрощается и принимает вид t_c=idem.

Б. Граничные условия второго рода, задающие величину плотности теплового потока для каждой точки поверхности и любого момента времени. Аналитически это можно представить следующим образом:

q_n = j(x, y, z, t), (4.17)

где q_n ¾ плотность теплового потока на поверхности тела.

В простейшем случае плотность теплового потока по поверхности и во времени остается постоянной q_n=idem. Такой случай теплообмена имеет место, например, при нагревании различных металлических изделий в высокотемпературных печах.

В. Граничные условия третьего рода, задающие температуру окружающей среды t_ж и закон теплообмена между поверхностью тела и окружающей средой. Для описания процесса теплообмена между поверхностью тела и средой используется закон Ньютона.

Согласно закону Ньютона, количество теплоты, отдаваемое единицей поверхности тела в единицу времени, пропорционально разности температур тела t_c и окружающей среды t_ж

q = a(t_c - t_ж). (4.18)

Коэффициент теплоотдачи харктеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоты, отдаваемому (или воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу.

Согласно закону сохранения энергии, количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи (4.18), должно равняться теплоте, подводимой к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела (4.7), т. е.

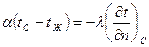, (4.19)

где n ¾ нормаль к поверхности тела; индекс «С» указывает на то, что температура и градиент относятся к поверхности тела (при n=0).

Окончательно граничное условие третьего рода можно записать в виде

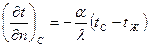. (4.20)

Уравнение (4.20), по существу, является частным выражением закона сохранения энергии для поверхности тела.

Г. Граничные условия четвертого рода, харктеризующие условия теплообмена системы тел или тела с окружающей средой по закону теплопроводности. Предполагается, что между телами осуществляется идеальный контакт (температуры соприкасающихся поверхностей одинаковы). В рассматриваемых условиях имеет место равенство тепловых потоков, проходящих через поверхность соприкосновения:

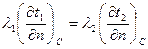. (4.21)