Процессы изменения состояния вещества
Задача 1. 1 кг метана при постоянной температуре t1=20°C и начальном давлении Р1=3,0 МПа сжимается до давления Р2=5,8 МПа. Определить удельный конечный объем, количество тепла, отводимого в процессе сжатия, и затрачиваемую работу.
Решение. По уравнению состояния находим удельный начальный объем газа, предварительно определив газовую постоянную метана:
Дж/(кг×К),
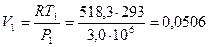м3/кг.
Так как процесс сжатия газа по условию протекания изотермический (при постоянной температуре), когда n=1, P1V1=P2V2, то конечный объем газа
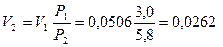м3/кг.
Работа, затрачиваемая на сжатие 1 кг газа, определяется из уравнения
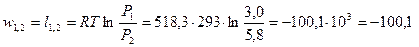кДж/кг.
Количество теплоты, отводимой от газа, численно равно работе, затраченной на сжатие. Следовательно, q= -100,1 кДж/кг.
Задача 2. Метан массой 1 кг адиабатически расширяется от давления Р1=5,4 МПа и температуры 40°С до давления Р2=1 МПа. Найти конечный объем, температуру, потенциальную и термодинамическую работу, изменение внутренней энергии и энтальпии. Показатель адиабаты принять равным 1,4.
Решение. Начальный удельный объем находится из уравнения Клапейрона. Газовая постоянная R=518,3 Дж/(кг×К).
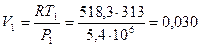м3/кг.
Для адиабатического процесса справедливы уравнения вида
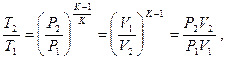
отсюда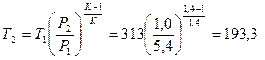 
К.
Конечный объем в процессе расширения равен:
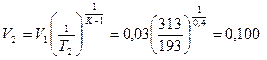м3/кг.
Определение удельных значений работ производим следующим образом:
термодинамическая работа
кДж/кг;
потенциальная работа
w1,2=K×l1,2=1,4×155,4=217,6 кДж/кг.
Изменение внутренней энергии и энтальпии в обратимом адиабатическом процессе соответственно равно термодинамической и потенциальной работам:
q1,2=0; DU1,2=-l1,2=-155,4 кДж/кг,
Dh1,2=-w1,2=-217,6 кДж/кг.
Дата добавления: 2015-10-13; просмотров: 1657;