Газовые смеси
Задача 1. По данным анализа установлен следующий объемный состав природного газа: СН4=96%; С2Н6=3%; С3Н8=0,3%; С4Н10=0,2%; СО2=0,1%; N2=0,4%. Определить среднюю молекулярную массу природного газа (mm), плотность газа в нормальных условиях (r), массовые концентрации компонентов (mi), их парциальные давления (Pi), средние теплоемкости (Сpm, Cvm) и показатель адиабаты.
Решение. Молекулярные массы составляющих смеси газов находим по данным физических характеристик компонентов газа из справочных таблиц:
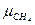 =16,04;
=16,04; 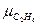 =30,07;
=30,07; 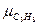 =44,09;
=44,09;
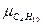 =58,12;
=58,12; 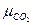 =44,01;
=44,01; 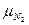 =28,02.
=28,02.
Молекулярная масса природного газа определяется по уравнению
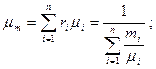
где mi — молекулярная масса компонентов смеси;
ri — молярная (объемная) концентрация компонентов смеси;
mi — массовая концентрация компонентов смеси.
Так как в условии задачи дан объемный состав газа, то удобнее воспользоваться первым уравнением соотношения:
 =0,96×16,04+0,03×30,07+0,003×44,09+0,002×58,12+
=0,96×16,04+0,03×30,07+0,003×44,09+0,002×58,12+
+0,001×44,01+0,004×28,02=16,704 (кг/кмоль).
Плотность газа при нормальных условиях (0°С и 0,1 МПа) можно определить из уравнения Клапейрона PV=RT или из закона Авогадро, утверждающего, что удельный молярный объем газа в нормальных условиях- величина постоянная и равна:
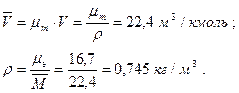
Из уравнения Клапейрона при t=0°C и Р=0,1 МПа
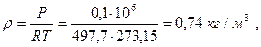
где 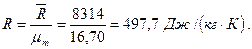
Массовые и объемные концентрации газа связаны между собой соотношением
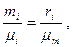 отсюда
отсюда 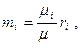
cледовательно, массовые концентрации отдельных компонентов смеси равны:
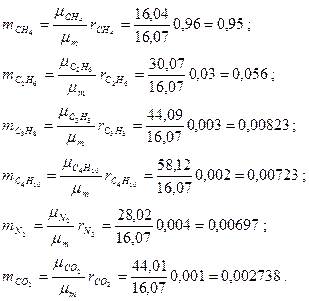
Сумма массовых концентраций, как и молярных (объемных), равна единице:
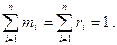
Парциальные давления отдельных компонентов газа определяются по закону Дальтона из соотношения Pi=ri×P. Находим давление каждого компонента, входящего в смесь:
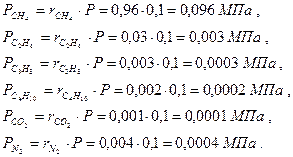
Сумма парциальных давлений равна давлению смеси:

Средняя теплоемкость смеси определяется по уравнениям:
массовая теплоемкость смеси: 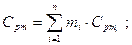
молярная теплоемкость смеси: 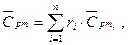
где 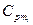 — массовая теплоемкость компонентов смеси при данной температуре;
— массовая теплоемкость компонентов смеси при данной температуре;
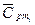 — молярная теплоемкость компонентов смеси при данной температуре.
— молярная теплоемкость компонентов смеси при данной температуре.
При температуре 0°С и давлении 0,1 МПа можно принять, что теплоемкость метана  = 2,17 кДж/(кг×К); этана
= 2,17 кДж/(кг×К); этана 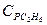 = 1,65 кДж/(кг×К); пропана
= 1,65 кДж/(кг×К); пропана 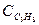 = 1,56 кДж/(кг×К); бутана
= 1,56 кДж/(кг×К); бутана 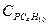 = 1,58 кДж/(кг×К); углекислого газа
= 1,58 кДж/(кг×К); углекислого газа 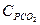 = 0,815 кДж/(кг×К); азота
= 0,815 кДж/(кг×К); азота 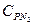 = 1,039 кДж/(кг×К). Следовательно, массовая теплоемкость смеси при постоянном давлении равна:
= 1,039 кДж/(кг×К). Следовательно, массовая теплоемкость смеси при постоянном давлении равна:
 0,95×2,17+0,056×1,65+0,008×1,56+0,007×1,58+
0,95×2,17+0,056×1,65+0,008×1,56+0,007×1,58+
+0,0027×0,815+0,0069×1,039=2,18 кДж/(кг×К).
Молярная теплоемкость смеси газов при постоянном давлении
 кДж/(кмоль×К).
кДж/(кмоль×К).
Из уравнения Майера  можно определить теплоемкость смеси при постоянном объеме:
можно определить теплоемкость смеси при постоянном объеме:
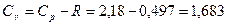 кДж/(кг×К);
кДж/(кг×К);
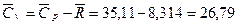 кДж/кг×К.
кДж/кг×К.
Показатель адиабаты природного газа указанного состава (как идеального газа)
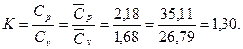
Задача 2. До какого давления необходимо сжать смесь газов, состоящую по весу из СО2=12%, О2=8%, N2=80%, чтобы при температуре t=20°С ее плотность была 1,6 кг/м3.
Решение. Находим молекулярную массу смеси через массовые концентрации компонентов смеси:
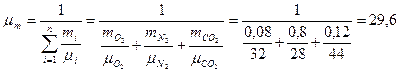 кг/кмоль.
кг/кмоль.
Давление смеси определим из уравнения состояния 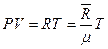 :
:
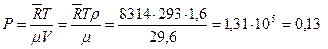 МПа.
МПа.
Задача 3. Определить весовой состав газовой смеси, состоящей из углекислоты СО2 и азота N2, если известно, что парциальное давление углекислого газа 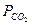 =1,1 ат, а давление смеси равно 3 ат.
=1,1 ат, а давление смеси равно 3 ат.
Решение. Определим парциальное давление азота:
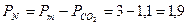 ат.
ат.
Объемная концентрация азота по закону Дальтона
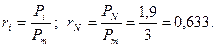
Объемная концентрация углекислого газа
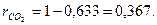
Молекулярная масса смеси
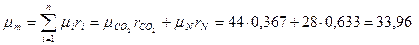 кг/кмоль.
кг/кмоль.
Используя соотношение mi/mm=mi/ri, определим весовую концентрацию азота и углекислого газа:

Проверка: 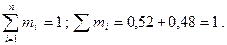
Дата добавления: 2015-10-13; просмотров: 6421;
