Уравнение колебаний струны

Определение. В математической физике струной называется тонкая нить, в которой возможно возникновение напряжений только в продольном, но не в поперечном направлении.

Пусть концы натянутой струны закреплены в точках х = а и x = b, возникающие в ней напряжения обозначим Т. Будем также считать, что плотность струны постоянна на всем ее протяжении.

Допустим, что в момент t₀ = 0 струна выведена из состояния равновесия и совершает малые колебания.

Отклонение струны в каждой точке с координатой х в момент времени t обозначим как

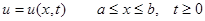
u

C

B a

A

D

0 a x x+Dx b x

На произвольный элемент длины нити (х, х + Dх) действуют две силы натяжения

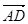и 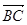. При этом:

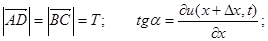
Если считать колебания малыми, то можно принять:

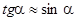
Тогда проекция силы 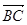на ось u:

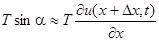
Проекция силы 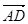на ось u:

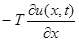
Находим сумму этих проекций:

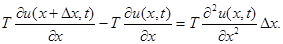
Выражение, стоящее в правой части равенства получено в результате применения теоремы Лагранжа к выражению, стоящему слева.

Произведение массы на ускорение рассматриваемого элемента струны равно:

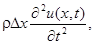
где r — плотность струны.

Приравнивая полученное выражение к значению проекции силы, получим:

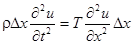
Или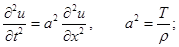

Для полного определения движения струны полученного уравнения недостаточно. Функция u(x, t) должна еще удовлетворять граничным условиям, описывающим состояние струны на концах (в точках x = a и x = b) и начальнымусловиям, описывающим состояние струны в момент времени t = 0.

Совокупность граничных и начальных условий называется краевымиусловиями.

Таким образом, задача Коши состоит в нахождении решения линейного дифференциального уравнения с частными производными второго порядка при начальных условиях

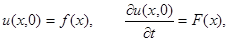
и краевых условиях

.

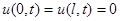Начальные условия показывают, в каком положении находится струна в начальный момент времени и скорость каждой ее точки в начальный момент времени.

Функции f(x) и F(x) заданы.

Краевые условия показывают, что концы струны закреплены в точках a = 0, b = l