Уравнение теплопроводности

Температуру физического тела в произвольной точке с координатами (x, y, z) в момент времени t можно представить в виде функции:

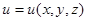
Составим дифференциальное уравнение:

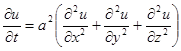
Выражение 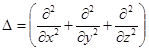называется оператором Лапласа.

Тогда составленное нами дифференциальное уравнение принимает вид:

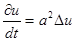
и называется уравнением теплопроводности в пространстве.

В качестве частных случаев рассматривают:

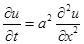— уравнение теплопроводности в стержне,

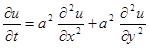— уравнение теплопроводности на плоскости.

В случае рассмотрения уравнения теплопроводности в стержне искомая функция u(x, t) должна удовлетворять записанному выше дифференциальному уравнению, начальному условию 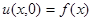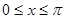и граничным условиям .

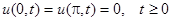В результате решения дифференциального уравнения методом Фурье получим:

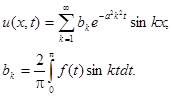
Отметим, что распространение тепла в теле называется стационарным, если функция u не зависит от времени t.