Решение задачи Коши методом Даламбера

Жан Лерон Д’Ламбер (1717–1783) — французский математик

В случае если длина струны очень велика, то на колебания, возникающие в середине струны, концы струны влияния практически не оказывают. Поэтому, рассматривая колебания бесконечной струны, уравнение

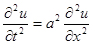
решается только при начальных условиях:

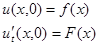
Для нахождения решения введем новые переменные:

Тогда исходное уравнение принимает вид:

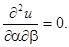
Решением этого уравнения будет функция 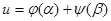, где j и y - некоторые функции, которые будем считать дважды дифференцируемыми.

Получаем: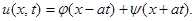

Если продифференцировать полученный ответ, получим:

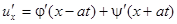
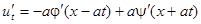
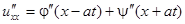
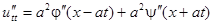
Т.е. .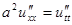

Далее с использованием начальных условий находим функции j и y.

Проинтегрировав последнее равенство на отрезке [0, x], получаем:

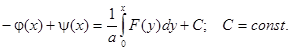
Тогда:

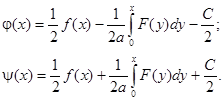
Решение задачи Коши получаем в виде:

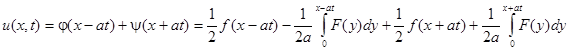
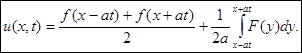
Эта формула называется формулой Даламбера.