Уравнения с разделяющимися переменными
Определение. Дифференциальное уравнение 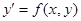 называется уравнением с разделяющимися переменными, если его можно записать в виде
называется уравнением с разделяющимися переменными, если его можно записать в виде
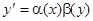 .
.
Такое уравнение можно представить также в виде:
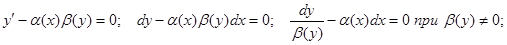
Перейдем к новым обозначениям 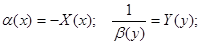
Получаем: 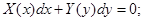

После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример. Найти общее решение дифференциального уравнения: 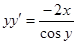
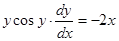
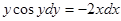

Интеграл, стоящий в левой части, берется по частям:

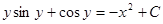
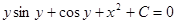
— это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
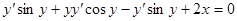
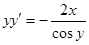 — верно
— верно
Пример. Найти решение дифференциального уравнения 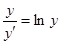 при условии у(2) = 1.
при условии у(2) = 1.
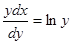
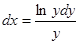
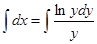
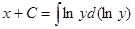

при у(2) = 1 получаем 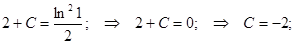
Итого:  или
или 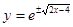 — частное решение;
— частное решение;
Проверка: 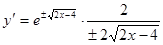 , итого
, итого
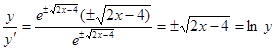 — верно.
— верно.
Пример. Решить уравнение 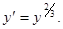
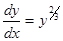
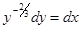
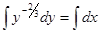
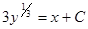
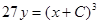 — общий интеграл
— общий интеграл
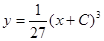 — общее решение
— общее решение
Пример. Решить уравнение 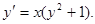
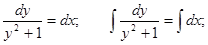
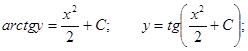
Пример. Решить уравнение 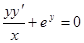 при условии у(1) = 0.
при условии у(1) = 0.

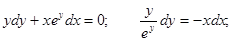
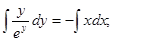
Интеграл, стоящий в левой части будем брать по частям.
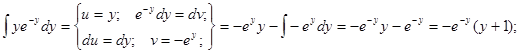
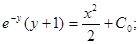

Если у(1) = 0, то 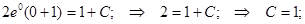
Итого, частный интеграл: 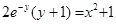 .
.
Пример. Решить уравнение 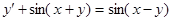 .
.
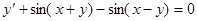
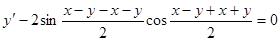
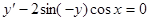
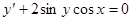
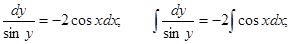
Получаем общий интеграл:
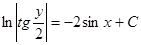
Пример. Решить уравнение 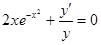
Преобразуем заданное уравнение:
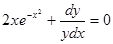
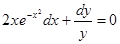
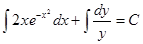
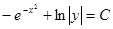
Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.
Пример. Решить уравнение 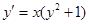 .
.
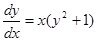
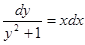
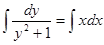 ;
; 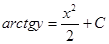 ;
;
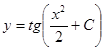
Допустим, заданы некоторые начальные условия х0 и у0. Тогда:
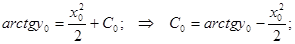
Получаем частное решение 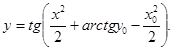
Дата добавления: 2015-10-13; просмотров: 602;
