Уравнения, приводящиеся к однородным

Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.

Это уравнения вида .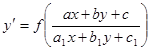

Если определитель 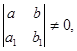то переменные могут быть разделены подстановкой

где a и b - решения системы уравнений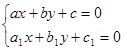

Пример. Решить уравнение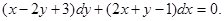

Получаем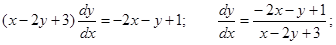

Находим значение определителя .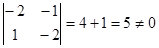

Решаем систему уравнений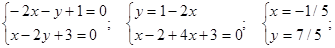

Применяем подстановку 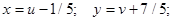в исходное уравнение:

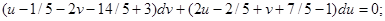
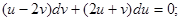
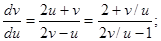
Заменяем переменную при подстановке в выражение, записанное выше, имеем:

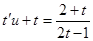
Разделяем переменные: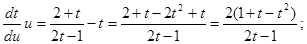

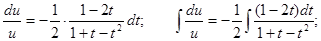
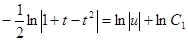
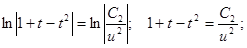
Переходим теперь к первоначальной функции у и переменной х.

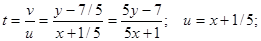
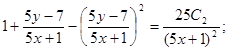
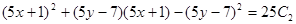
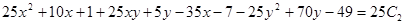
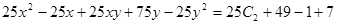
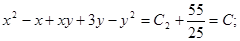
Итого, выражение является общим интегралом исходного дифференциального уравнения.

В случае если в исходном уравнении вида 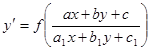определитель 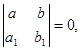то переменные могут быть разделены подстановкой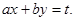

Пример. Решить уравнение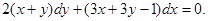

Получаем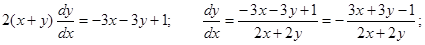

Находим значение определителя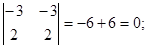

Применяем подстановку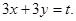

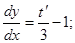
Подставляем это выражение в исходное уравнение:

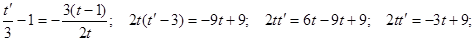
Разделяем переменные: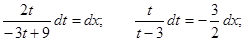

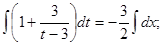
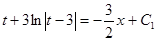
Далее возвращаемся к первоначальной функции у и переменной х.

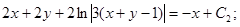
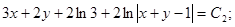
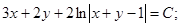
таким образом, мы получили общий интеграл дифференциального уравнения.