Лекция 9. Линейная модель экономики и балансовое уравнение (модели Леонтьева). Решение балансового уравнения, экономический смысл матрицы .
Одна из простейших моделей процесса обмена в хозяйстве может быть описана следующим образом. Имеется n технологических процессов (или отраслей), при помощи каждого из которых производится некоторый продукт. Пусть 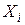 означает суммарный выпуск отрасли i,
означает суммарный выпуск отрасли i, 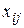 представляет общее количество продукта отрасли i, потребляемое отраслью j,
представляет общее количество продукта отрасли i, потребляемое отраслью j, 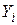 будут выражать разности между суммарным выпуском отрасли i и количеством продукта этой отрасли, потребленным n отраслями. Величину
будут выражать разности между суммарным выпуском отрасли i и количеством продукта этой отрасли, потребленным n отраслями. Величину 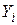 обычно называют конечным спросом для продукта i.
обычно называют конечным спросом для продукта i.
Так как валовой объем продукции любой i-ой отрасли равен суммарному объему продукции, потребляемой всеми n отраслями, и конечного продукта, то должно выполняться соотношение
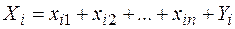 (i = 1, 2,… n),
(i = 1, 2,… n),
или, в сокращенной форме
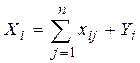 или
или 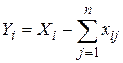 (i = 1, 2,… n) (1)
(i = 1, 2,… n) (1)
Уравнения (1) (их n штук) называются соотношениями межотраслевого баланса. Единицы измерения содержащихся в уравнениях (1) величин могут быть натуральными и для каждого уравнения свои (кубометры, тонны, штуки и т.п.). Но они могут быть и универсальными (стоимостными). В зависимости от этого различают натуральный и стоимостной межотраслевые балансы. Для определенности рассмотрим далее стоимостной баланс (все величины, входящие в уравнения (1), выражены в рублях).
В замкнутой модели Леонтьева для всех i. Иными словами, никаких избытков нет. Если в качестве одной из отраслей фигурирует труд, то вся рабочая сила используется полностью. Если другим типом отрасли, например, сталелитейная, то вся произведенная сталь потребляется внутри системы. Замкнутые модель, как правило включает такие отрасли, как услуги, управление, производство сырья.
В открытой модели Леонтьева по крайней мере для одного i. С экономической точки зрения открытая модель предполагает наличие внешнего фактора – некоторого количества капитала, труда, сырья и т.п., привносимого в систему извне. Существенной характеристикой открытой модели является существование внешнего спроса или внешнего предложения или того и другого вместе.
Введем коэффициенты прямых затрат 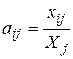 . Введенные таким образом величины можно интерпретировать как количества продукта отрасли i, необходимые для производства единицы продукта j. С другой стороны
. Введенные таким образом величины можно интерпретировать как количества продукта отрасли i, необходимые для производства единицы продукта j. С другой стороны 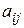 называются производственными (или технологическими) коэффициентами. показывающие затраты i-ой отрасли на производство единицы продукции j-ой отрасли. То есть aij – стоимость продукции отрасли i, вложенной в 1 рубль продукции отрасли j. Так как эти коэффициенты зависят в основном от существующей технологии производства в производящих отраслях, а эта технология меняется достаточно медленно и за рассматриваемый относительно короткий период времени может считаться неизменной, то их можно считать постоянными. Это означает линейную зависимость объема xij продукции i-ой отрасли, потребляемой j-ой отраслью, от валового объема xj j-ой отрасли:
называются производственными (или технологическими) коэффициентами. показывающие затраты i-ой отрасли на производство единицы продукции j-ой отрасли. То есть aij – стоимость продукции отрасли i, вложенной в 1 рубль продукции отрасли j. Так как эти коэффициенты зависят в основном от существующей технологии производства в производящих отраслях, а эта технология меняется достаточно медленно и за рассматриваемый относительно короткий период времени может считаться неизменной, то их можно считать постоянными. Это означает линейную зависимость объема xij продукции i-ой отрасли, потребляемой j-ой отраслью, от валового объема xj j-ой отрасли:
Сделаем подстановку 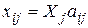 в равенство (1). Отсюда следует, что
в равенство (1). Отсюда следует, что 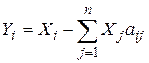
 или в матричном виде :
или в матричном виде :
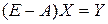 (2)
(2)
Такое уравнение еще носит название балансового уравнения. Его решение можно найти с помощью обратной матрицы.
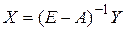 .
.
Матрица 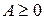 (матрица прямых затрат) называется продуктивной, если для любого вектора
(матрица прямых затрат) называется продуктивной, если для любого вектора 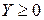 существует решение
существует решение 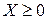 балансового уравнения. Матрица А продуктивна, если
балансового уравнения. Матрица А продуктивна, если 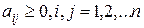 ;
; 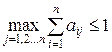 и существует номер j такой, что
и существует номер j такой, что 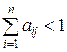 .
.
Чистой продукцией отрасли называется разность между валовой продукцией этой отрасли и затратами продукции всех отраслей на производство этой отрасли.
Наиболее распространенной задачей, связанной с открытыми моделями Леонтьева, является следующая: считая величины 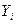 известными, найти
известными, найти 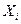 , удовлетворяющие соотношению (2). Рассмотрим эту задачу на простейшем примере.
, удовлетворяющие соотношению (2). Рассмотрим эту задачу на простейшем примере.
Предприятие производит три вида продукции в количестве 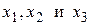 единиц каждого вида. Часть этой продукции расходуется внутри производства, а оставшаяся часть (товарная продукция) реализуется за пределами производства, Согласно равенству (2) составим систему уравнений:
единиц каждого вида. Часть этой продукции расходуется внутри производства, а оставшаяся часть (товарная продукция) реализуется за пределами производства, Согласно равенству (2) составим систему уравнений:
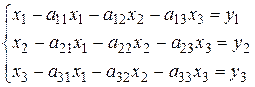
Здесь 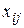 - количество продукции вида i, расходуемое на производство продукции вида j. Например
- количество продукции вида i, расходуемое на производство продукции вида j. Например 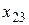 - количество продукции второго вида, расходуемое на производство продукции третьего вида. Технологический коэффициент
- количество продукции второго вида, расходуемое на производство продукции третьего вида. Технологический коэффициент 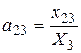 показывает сколько продукции второго вида расходуется при производстве продукции третьего вида. Перепишем систему в виде (2), где А – матрица, составленная из технологических коэффициентов, X – матрица, характеризующая выпуск продукции (производственный вектор) и Y - матрица, характеризующая товарную продукцию или конечный спрос. Это балансовое уравнение находит свое применение в планировании. Пусть мы имеем в своем распоряжении результаты деятельности предприятия за истекший период. Тогда мы можем составить балансовое уравнение и найти матрицу
показывает сколько продукции второго вида расходуется при производстве продукции третьего вида. Перепишем систему в виде (2), где А – матрица, составленная из технологических коэффициентов, X – матрица, характеризующая выпуск продукции (производственный вектор) и Y - матрица, характеризующая товарную продукцию или конечный спрос. Это балансовое уравнение находит свое применение в планировании. Пусть мы имеем в своем распоряжении результаты деятельности предприятия за истекший период. Тогда мы можем составить балансовое уравнение и найти матрицу 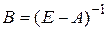 , которая называется матрицей полных производственных затрат. Элементы этой матрицы имеют вполне определенный экономический смысл:
, которая называется матрицей полных производственных затрат. Элементы этой матрицы имеют вполне определенный экономический смысл: 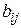 равен величине продукции i-го вида, необходимой для производства единицы товарной продукции j-го вида. Затем, зная величину конечного спроса на продукцию Y, на новый, производственный период, определим новый производственный вектор X .
равен величине продукции i-го вида, необходимой для производства единицы товарной продукции j-го вида. Затем, зная величину конечного спроса на продукцию Y, на новый, производственный период, определим новый производственный вектор X .
Разберем построение открытой модели и определим новый производственный план на примере.
Пример 1. Результаты деятельности некоторого предприятия, состоящего из трех цехов, каждый из которых производит свой вид продукции, представлены следующей таблицей.
| № цеха | Валовая продукция | Из нее использовано для производства продукции подразделениями | Конечная (товарная) продукция | ||
| - | |||||
| - |
Определить новый производственный план, учитывая, что 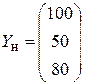
Решение.
Вычислим технологические коэффициенты и составим технологическую матрицу А.

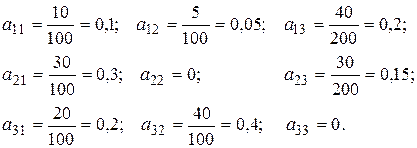
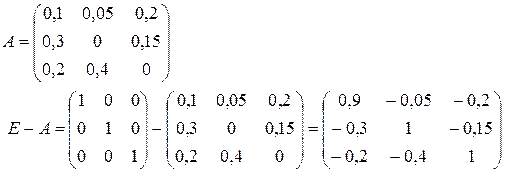
Вычислим матрицу полных производственных затрат 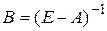 .
.
1) по формуле обратной матрицы: 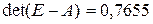 .
.
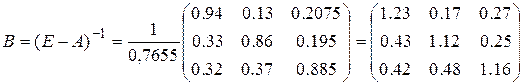
2) Если провести аналогию между суммой бесконечной геометрической прогрессии 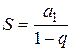 и
и 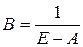 , то легко можно увидеть приближенную формулу: для вычисления
, то легко можно увидеть приближенную формулу: для вычисления 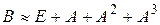 , как суммы бесконечной геометрической прогрессии с первым членом Е и знаменателем А.
, как суммы бесконечной геометрической прогрессии с первым членом Е и знаменателем А.

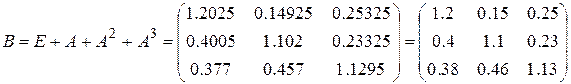
Определим новый производственный план, учитывая, что 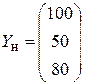
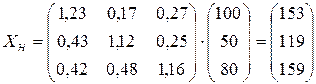
Использование приближенной матрицы В дает очень близкий результат.
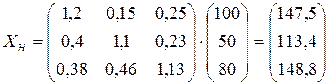 .
.
В соответствии с экономическим смыслом задачи искомые элементы 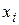 столбца X должны быть неотрицательны при любых неотрицательных значениях yi и aij (i = 1, 2,… n). В таком случае модель Леонтьева называется продуктивной.
столбца X должны быть неотрицательны при любых неотрицательных значениях yi и aij (i = 1, 2,… n). В таком случае модель Леонтьева называется продуктивной.
Существует несколько различных по форме критериев продуктивности модели Леонтьева. Один из них формулируется так (доказательство опускаем): если максимум сумм элементов столбцов матрицы A прямых затрат не превосходит единицы, то есть если 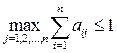 (2)
(2)
и существует номер j такой, что эта сумма строго меньше единицы
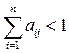 , (3)
, (3)
то модель Леонтьева является продуктивной. Отметим, что условия (2) и (3) естественны, так как они имеют наглядный экономический смысл. Действительно,
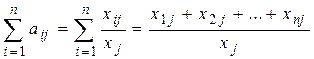 – (4)
– (4)
– это доля, которую составляет суммарная стоимость продукции всех отраслей, вложенная в продукцию j-ой отрасли, по отношению к общей стоимости продукции j-ой отрасли. И эта доля для любой отрасли, естественно, не должна превосходить единицу. А точнее, для рентабельной отрасли должна быть меньше единицы, ибо общая стоимость xj продукции j-ой отрасли включает в себя и другие затраты – стоимость рабочей силы, амортизацию основных фондов и т.д., а также прибыль, получаемую отраслью от продажи продукции.
Разберем еще один пример.
Пример 2. В таблице ниже содержатся данные баланса промышленности и сельского хозяйства в некотором регионе за некоторый период (в миллиардах рублей):
| Отрасль производства | Производственное потребление | Конечный продукт | Валовой выпуск | |
| Промышленность | Сельское хозяйство | |||
| Промышленность | 0,7 | 2,1 | 7,2 | |
| Сельское xоз-во | 1,2 | 1,5 | 12,3 |
Требуется вычислить необходимый объем валового выпуска каждой отрасли, если конечный продукт промышленности увеличится вдвое, а сельского хозяйства останется на прежнем уровне.
Решение. Согласно таблицы имеем:
| x11 = 0,7; | x12 = 2,1; | x21 = 1,2; | x22 = 1,5; |
| x1 = 10; | x2 = 15; | y1 = 7,2; | y2 = 12,3. |
По формуле 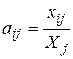 находим коэффициенты прямых затрат:
находим коэффициенты прямых затрат:
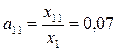 ;
; 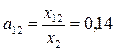 ;
; 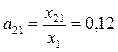 ;
; 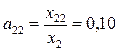
Таким образом, матрица А прямых затрат
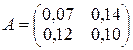
имеет неотрицательные элементы и, очевидно, удовлетворяет критерию продуктивности, выражаемому неравенствами (2) и (3), ибо
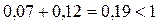 ;
; 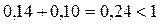 .
.
По условию задачи, в измененных условиях производства конечный продукт промышленности y1 должен составить 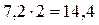 млрд. рублей, а конечный продукт y2 сельского хозяйства должен остаться неизменным и составить 12,3 млрд. рублей. Поэтому для определения соответствующих валовых объемов x1 и x2 этих отраслей получаем, следующую систему линейных уравнений 2-го порядка:
млрд. рублей, а конечный продукт y2 сельского хозяйства должен остаться неизменным и составить 12,3 млрд. рублей. Поэтому для определения соответствующих валовых объемов x1 и x2 этих отраслей получаем, следующую систему линейных уравнений 2-го порядка:
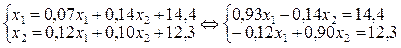
Ее главный определитель
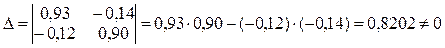
Значит, система имеет единственное решение. Вычисляя еще два определителя неизвестных
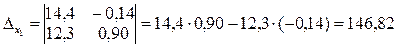
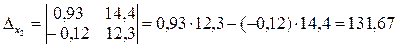
и используя формулы Крамера, получим:
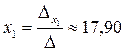 ;
; 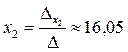 .
.
Дата добавления: 2015-10-05; просмотров: 3033;
