Уравнение любой волны является решением дифференциального уравнения, называемого волновым.
Чтобы установить вид этого уравнения составим второе. Частные производные по координатам и времени от ф[X].
Продифференцировав эту функцию дважды по каждой из переменных, получим:
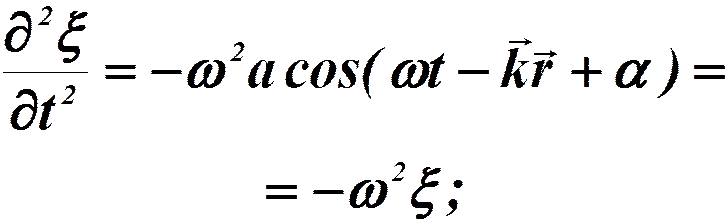

Сложим:
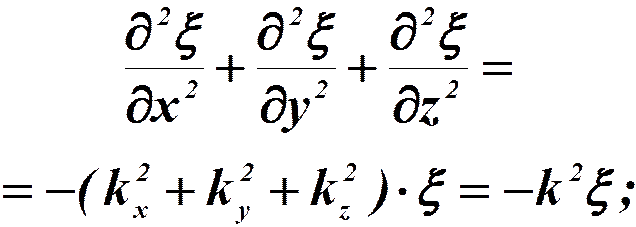
Заменим:

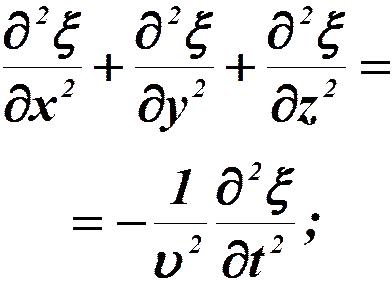
Волновое уравнение:
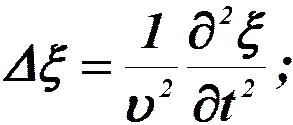
Δ – оператор Лапласа;
Волновому уравнению удовлетворяет функция вида:
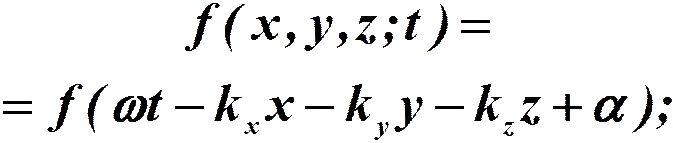
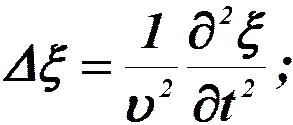
υ – фазовая скорость;
Для плоской волны, вдоль оси x, волновое уравнение имеет вид:
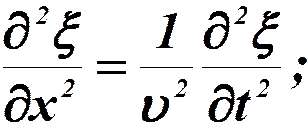
Дата добавления: 2015-10-13; просмотров: 737;
