Уравнение плоской и сферической волны.
Уравнением волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат (x, y, z) и t:
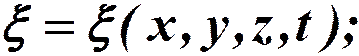
Колебания точек в плоскости x=0:
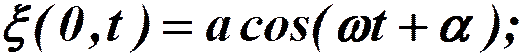
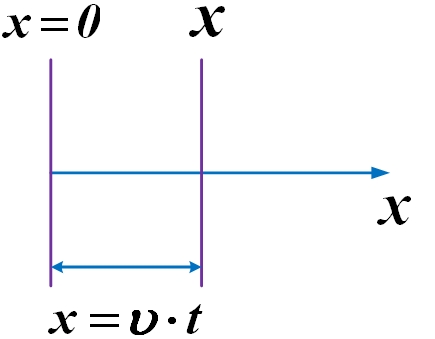
Для произвольного x:
Колебания частиц, лежащих в плоскости x будут отставать по времени на τ от колебаний частиц, лежащих в плоскости x=0:

Итак, уравнение плоской волны (и продольной и поперечной) вдоль оси x:
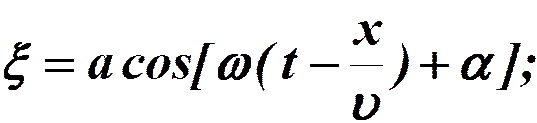
зафиксируем значение фазы:

Это связь t и x, в котором фаза имеет фиксированное значение. 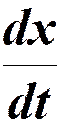 - дает скорость, с которой перемещается данное значение фазы.
- дает скорость, с которой перемещается данное значение фазы.

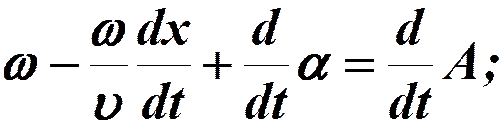
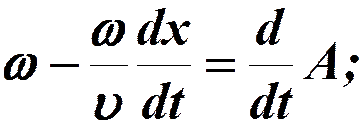
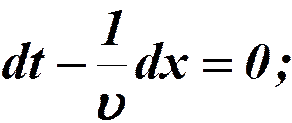
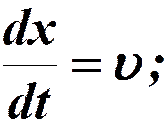
Скорость распространения волны – это скорость распространения фазы (фазовая скорость).
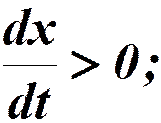
Для волны в противоположном напрвлении:

Уравнению плоской волны можно придать симметричный относительно x и t вид:
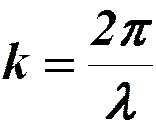 - волновое число;
- волновое число;
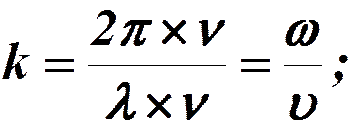
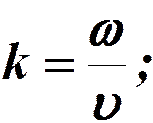
тогда:
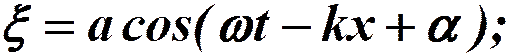
3. Уравнение для волны, образующей с осями x, y, z углы α, β, γ.
Колебания в начале координат:
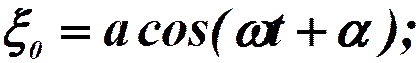
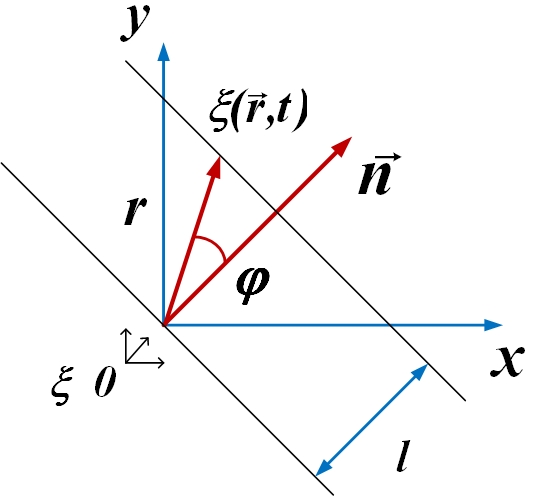
Возьмем волновую поверхность, отстоящую от начала координат на l. Колебания в ней будут отставать от начального на время 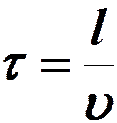 :
:
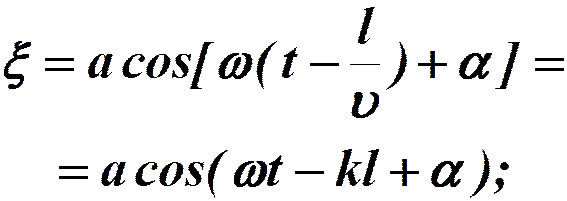
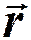 - радиус – вектор произвольной точки;
- радиус – вектор произвольной точки;
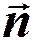 - единичный вектор нормали к волновой поверхности.
- единичный вектор нормали к волновой поверхности.

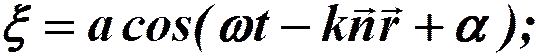
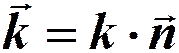 - волновой вектор, нормаль к волновой поверхности.
- волновой вектор, нормаль к волновой поверхности.
Уравнение плоской незатухающей волны в направлении волнового вектора:
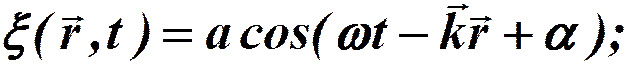
Для затухающих волн надо добавить множитель:
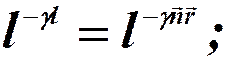
Перейдем от радиус – вектора 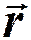 к координатам x, y, z:
к координатам x, y, z:
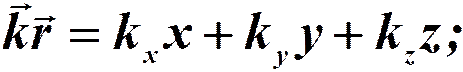 тогда:
тогда:
(X) 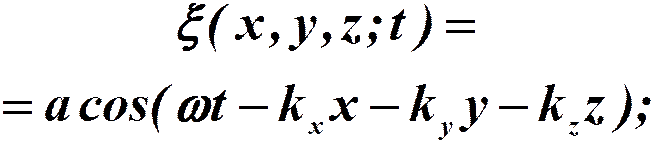
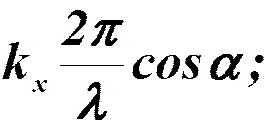

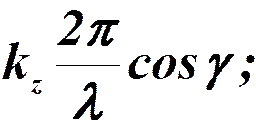
Запись в комплексной форме:
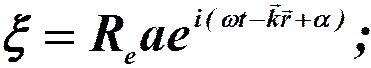
 - комплексная амплитуда;
- комплексная амплитуда;
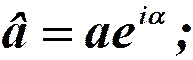
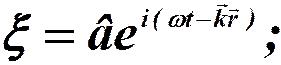
 - опускают.
- опускают.
Дата добавления: 2015-10-13; просмотров: 856;
