Лекция 9. Экспериментальное обоснование основных идей квантовой теории.

План лекции:

1. Фотоэффект. Уравнение Эйнштейна.
2. Законы внутреннего и внешнего фотоэффекта.

ТЕЗИСЫ

Немецкие физики Д. Франк и Г. Герц, изучая методом задерживающего потен­циала столкновения электронов с атомами газов (1913 г.), экспериментально доказали дискретность значений энергии атомов. Принципиальная схема их установки при­ведена на рис. 292. Вакуумная трубка, заполненная парами ртути (давление при­близительно равно 13 Па), содержала ка­тод (К), две сетки (C₁ и С₂) и анод (А). Электроны, эмиттируемые катодом, уско­рялись разностью потенциалов, приложен­ной между катодом и сеткой С₁ Между сеткой С2 и анодом приложен небольшой (примерно 0,5 В) задерживающий потен­циал. Электроны, ускоренные в области /, попадают в область 2 между сетками, где испытывают соударения с атомами паров ртути. Электроны, которые после соударе­ний имеют достаточную энергию для прео­доления задерживающего потенциала в области 3, достигают анода. При неупру­гих соударениях электронов с атомами ртути последние могут возбуждаться. Со­гласно боровской теории, каждый из ато­мов ртути может получить лишь вполне определенную энергию, переходя при этом в одно из возбужденных состояний. Поэто­му если в атомах действительно существу­ют стационарные состояния, то электроны, сталкиваясь с атомами ртути, должны те­рять энергию дискретно, определенными порциями, равными разности энергий со­ответствующих стационарных состояний атома.

Из опыта следует, что при увеличении ускоряющего потенциала вплоть до 4,86 В анодный ток возрастает монотонно, его значение проходит через максимум (4,86 В), затем резко умень­шается и возрастает вновь. Дальнейшие максимумы наблюдаются при 2•4,86 и 3•4,86 В.

Ближайшим к основному, невозбуж­денному, состоянию атома ртути является возбужденное состояние, отстоящее от ос­новного по шкале энергий на 4,86 эВ. Пока разность потенциалов между като­дом и сеткой меньше 4,86 В, электроны, встречая на своем пути атомы ртути, ис­пытывают с ними только упругие соударения. При ej=4,86 эВ энергия электрона становится достаточной, чтобы вызвать неупругий удар, при котором электрон отдает атому ртути всю кинетическую энергию, возбуждая переход одного из электронов атома из нормального энерге­тического состояния на возбужденный энергетический уровень. Электроны, поте­рявшие свою кинетическую энергию, уже не смогут преодолеть тормозящего поля и достигнуть анода. Этим и объясняется первое резкое падение анодного тока при ej=4,86 эВ. При значениях энергии, кратных 4,86 эВ, электроны могут испы­тать с атомами ртути 2, 3, ... неупругих соударения, потеряв при этом полностью свою энергию, и не достигнуть анода, т. е. должно наблюдаться резкое падение анодного тока. Это действительно наблю­дается на опыте.

Таким образом, опыты Франка и Герца показали, что электроны при столкновении с атомами ртути передают атомам только определенные порции энергии, причем 4,86 эВ — наименьшая возможная порция энергии (наименьший квант энергии), ко­торая может быть поглощена атомом рту­ти в основном энергетическом состоянии. Следовательно, идея Бора о существова­нии в атомах стационарных состояний блестяще выдержала экспериментальную проверку.

Атомы ртути, получившие при соуда­рении с электронами энергию DE, перехо­дят в возбужденное состояние и должны возвратиться в основное, излучая при этом, согласно второму постулату Бора, световой квант с часто­той n=DE/h. По известному значению DE=4,86 эВ можно вычислить длину волны излучения: l=hc/DE»255 нм. Та­ким образом, если теория верна, то атомы ртути, бомбардируемые электронами с энергией 4,86 эВ, должны являться источ­ником ультрафиолетового излучения с l»255 нм. Опыт действительно обнаружи­вает одну ультрафиолетовую линию с l»254 нм. Таким образом, опыты Франка и Герца экспериментально подтвердили не только первый, но и второй постулат Бора. Эти опыты сыграли огромное значение в развитии атомной физики.

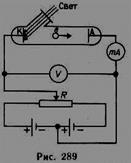
Гипотеза Планка получила подтверждение и дальнейшее развитие при объяснении фотоэффекта — явления, открытие и исследование которо­го сыграло важную роль в становлении квантовой теории. Различают фотоэффект внешний, внутренний и вентильный. Внеш­ним фотоэлектрическим эффектом (фото­эффектом) называется испускание элек­тронов веществом под действием элек­тромагнитного излучения. Фотоэф­фект обнаружен (1887 г.) Г.Герцем. Первые фундаментальные исследова­ния фотоэффекта выполнены А.Г.Столетовым (рис. 289).

Облучая катод светом различных длин волн, Столетов установил следующие за­кономерности, не утратившие своего зна­чения до нашего времени: 1) наиболее эффективное действие оказывает ультра­фиолетовое излучение; 2) под действием света вещество теряет только отрицатель­ные заряды; 3) сила тока, возникающего под действием света, прямо пропорцио­нальна его интенсивности.

Зависимость, соответствующая двум различным освещенностям Е_е катода (частота света в обоих случаях одинакова), приведена на рис. 290. По мере увеличения U фототок постепенно возрастает, т. е. все большее число фотоэлектронов достигает анода. Максимальное значение тока I_нас — фототок насыщения — опреде­ляется таким значением U, при котором все электроны, испускаемые катодом, до­стигают анода: I_нас=en, где n — число электронов, испускаемых катодом в 1 с.

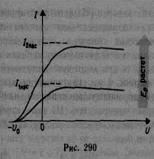
Из вольт-амперной характеристики следует, что при U=0фототок не исчеза­ет. Следовательно, электроны, выбитые светом из катода, обладают некоторой на­чальной скоростью v, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Для того чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение u₀. При U=U₀ни один из электронов, даже обладающий при вылете из катода максимальной скоростью v_max, не может преодолеть задерживающего по­ля и достигнуть анода. Следовательно, mv²_max/2=eU₀, (202.1), т. е., измерив задерживающее напряжение U_0,можно определить максимальные зна­чения скорости и кинетической энергии фотоэлектронов.

Три закона внешнего фотоэффекта.

I. Закон Столетова: при фиксирован­ной частоте падающего света число фото­электронов, вырываемых из катода в еди­ницу времени, пропорционально интенсив­ности света (сила фототока насыщения пропорциональна энергетической осве­щенности E_е катода).

II. Максимальная начальная ско­рость (максимальная начальная кинети­ческая энергия) фотоэлектронов не за­висит от интенсивности падающего све­та, а определяется только его частотой n, а именно линейно возрастает с увели­чением частоты.

III. Для каждого вещества существует «красная граница» фотоэффекта, т. е. ми­нимальная частота n₀ света (зависящая от химической природы вещества и состояния его поверхности), при которой свет лю­бой интенсивности фотоэффекта не вызы­вает.

А.Эйнштейн в 1905 г. показал, что явле­ние фотоэффекта и его закономерности могут быть объяснены на основе предло­женной им квантовой теории фотоэффек­та. Согласно Эйнштейну, свет частотой n не только испускается, как это предпола­гал Планк, но и распространя­ется в пространстве и поглощается ве­ществом отдельными порциями (кванта­ми), энергия которых e₀=hn. Таким образом, распространение света нужно рассматривать не как непрерывный волно­вой процесс, а как поток локализованных в пространстве дискретных световых кван­тов, движущихся со скоростью с распро­странения света в вакууме. Эти кванты электромагнитного излучения получили название фотонов.

По Эйнштейну, каждый квант погло­щается только одним электроном. Поэтому число вырванных фотоэлектронов должно быть пропорционально интенсивности све­та. Безынерционность фотоэффекта объясняется тем, что передача энергии при столкновении фото­на с электроном происходит почти мгно­венно. Энергия падающего фотона расходует­ся на совершение электроном работы вы­хода А из металла и на со­общение вылетевшему фотоэлектрону ки­нетической энергии mv²_max/2. По закону сохранения энергии, hn=A+mv²_max/2, что называется уравнением Эйнштейна для внешнего фотоэффекта. Согласно изложенному, получим, что n₀=A/h и есть «красная граница» фотоэффекта для данного металла. Она зависит лишь от работы выхода электрона, т. е. от химиче­ской природы вещества и состояния его поверхности. Это выражение можно записать в виде eU₀=h(n-n₀)