Лекция 11. Корпускулярно-волновой дуализм

План лекции:

1. Корпускулярно-волновой дуализм.
2. Гипотеза де Бройля. Принцип соответствия. Статистический смысл волновой функции. Соотношение неопределенностей. Волновые свойства микрочастиц и соотношение неопределенностей.

ТЕЗИСЫ

1. Излучение черного тела, фотоэффект, эф­фект Комптона служат доказательст­вом квантовых пред­ставлений о свете. С другой стороны, интерференция, дифракция и поляризация света подтверждают волно­вую природу света. Наконец, давление и преломление света объясняются как волновой, так и кванто­вой теориями. Таким образом, электромаг­нитное излучение обнаруживает единство взаимо­исключающих свойств — непрерывных (во­лны) и дискретных (фотоны), которые взаимно дополняют друг друга. Основные уравнения, свя­зывающие корпускулярные свойства элек­тромагнитного излучения (энергия и им­пульс фотона) с волновыми свойствами (частота или длина волны): e_g=hn, p_g=hn/c=h/l.

Более детальное рассмотрение оптиче­ских явлений приводит к выводу, что свой­ства непрерывности, характерные для электромагнитного поля световой волны, не следует противопоставлять свойствам дискретности, характерным для фотонов. Свет, обладая одновременно корпускуляр­ными и волновыми свойствами, обнаружи­вает определенные закономерности в их проявлении. Так, волновые свойства света проявляются в закономерностях его рас­пространения, интерференции, дифракции, поляризации, а корпускулярные — в про­цессах взаимодействия света с веществом. Чем больше длина волны, тем меньше энергия и импульс фотона и тем труднее обна­руживаются квантовые свойства света (с этим связано, например, существование «красной границы» фотоэффекта). Наобо­рот, чем меньше длина волны, тем больше энергия и импульс фотона и тем труднее обнаруживаются волновые свойства света (например, волновые свойства (дифрак­ция) рентгеновского излучения обнаруже­ны лишь после применения в качестве диф­ракционной решетки кристаллов).

Взаимосвязь между двойственными корпускулярно-волновыми свойствами света можно объяснить, если использо­вать, как это делает квантовая оптика, статистический подход к рассмотрению за­кономерностей распространения света: квадрат амплиту­ды световой волны в данной точке про­странства является мерой вероятности по­падания фотонов в данную точку.

Французский ученый Луи де Бройль, осознавая существующую в природе симметрию и развивая представ­ления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль ут­верждал, что не только фотоны, но и элек­троны и любые другие частицы материи наряду с корпускулярными обладают так­же волновыми свойствами.

Согласно де Бройлю, с каждым микрообъектом связываются, с одной сто­роны, корпускулярные характеристики — энергия Е и импульс р, а с другой — волновые характеристики — частота v и длина волны К. Количественные соотно­шения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов: E=hv, p=h/l. (213.1). Смелость гипотезы де Бройля заключа­лась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопо­ставляют волновой процесс с длиной вол­ны, определяемой по формуле де Бройля: l=h/p (213.2). Это соотношение справедливо для любой частицы с импульсом р.

Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что перед нами универсальное явление, общее свойство материи. Но тогда волновые свойства до­лжны быть присущи и макроскопическим телам. Представление о двойственной корпускулярно-волновой природе частиц ве­щества углубляется еще тем, что на части­цы вещества переносится связь между полной энергией частицы и частотой v волн де Бройля: e=hv (213.3). Это свидетельствует о том, что соотноше­ние между энергией и частотой имеет характер универсального соотношения, справедливого как для фо­тонов, так и для любых других микроча­стиц.

Подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме свойств вещества корен­ным образом изменила представления о свойствах микрообъектов. Всем микро­объектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни части­цей, ни волной в классическом понимании.

Рассмотрим свободно движущуюся со ско­ростью v частицу. Групповая скорость волн де Бройля равна скорости частицы. Групповая скорость фотона u=pc²/E=тсс²/mc²=c , т. е. равна скорости самого фотона. Волны де Бройля испытывают диспер­сию. Это обстоятельство сыграло в свое время большую роль в развитии положе­ний квантовой механики.

Согласно двойственной корпускулярно-волновой природе частиц вещества, для опи­сания микрочастиц используются то волновые, то корпускулярные представления. Поэтому приписывать им все свойст­ва частиц и все свойства волн нельзя. В классической механике всякая частица движется по определенной тра­ектории, так что в любой момент времени точно фиксированы ее координата и им­пульс. Микрочастицы из-за наличия у них волновых свойств существенно отличают­ся от классических частиц. Одно из основ­ных различий заключается в том, что не­льзя говорить о движении микрочастицы по определенной траектории и неправо­мерно говорить об одновременных точных значениях ее координаты и импульса. Это следует из корпускулярно-волнового дуа­лизма. Согласно соотношению неопределенностей Гейзенберга, микроча­стица (микрообъект) не может иметь од­новременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (р_х, р_у, р_z), причем не­определенности этих величин удовлетворя­ют условиям

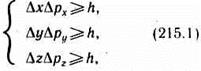
т. е. произведение неопределенностей ко­ординаты и соответствующей ей проекции импульса не может быть меньше величины порядка h. Для микрочастицы не существует состояний, в которых ее ко­ординаты и импульс имели бы одновремен­но точные значения. Отсюда вытекает и фактическая невозможность одновре­менно с любой наперед заданной точно­стью измерить координату и импульс микрообъекта.

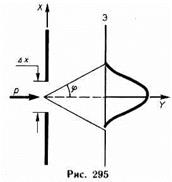
Пусть поток электронов проходит через узкую щель шириной Dх, распо­ложенную перпендикулярно направлению их движения (рис.295). Дифракционная карти­на, наблюдаемая на экране (Э), характеризует­ся главным максимумом, расположенным сим­метрично оси Y, и побочными максимумами по обе стороны от главного. До прохождения через щель электроны дви­гались вдоль оси К, поэтому составляющая им­пульса р_x=0, так что Dр_x=0, а координа­та х частицы является совершенно неопреде­ленной. В момент прохождения электронов через щель их положение в направлении оси X определяется с точностью до ширины щели, т. е. с точностью Dx. В этот же момент вследствие дифракции электроны отклоняются от первоначального направления и будут дви­гаться в пределах угла 2j (j — угол, соответ­ствующий первому дифракционному миниму­му). Следовательно, появляется неопределен­ность в значении составляющей импульса вдоль оси X, которая, как следует из рис. 295 и форму­лы (213.1), равна Dр_х=рsinj=(h/l)sinj. (215.2) Для простоты ограничимся рассмотрением только тех электронов, которые попадают на экран в пределах главного максимума. Из тео­рии дифракции известно, что первый минимум соответствует углу j, удовлетворяю­щему условию Dxsinj=l, (215.3), где Dx — ширина щели, а l - длина волны де Бройля. Из формул получим DxDp_x=h. Следовательно, получаем выражение DxDp_x³h, т.е. соотношение неопределенностей.

Невозможность одновременно точно определить координату и соответствую­щую составляющую импульса не связана с несовершенством методов измерения или измерительных приборов, а является след­ствием специфики микрообъектов, отра­жающей особенности их объективных свойств, а именно двойственной корпускулярно-волновой природы. Соотношение не­определенностей получено при одновре­менном использовании классических ха­рактеристик движения частицы (коорди­наты, импульса) и наличия у нее волновых свойств. Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопре­деленностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.

Соотношение неопределенностей, отра­жая специфику физики микрочастиц, по­зволяет оценить, например, в какой мере можно применять понятия классической механики к микрочастицам, в частности с какой степенью точности можно гово­рить о траекториях микрочастиц. Извест­но, что движение по траектории характе­ризуется в любой момент времени опреде­ленными значениями координат и скоро­сти. Выразим соотношение неопределенно­стей (215.1) в виде DxDv_x³h/m. (215.4)

Из этого выражения следует, что чем больше масса частицы, тем меньше не­определенности ее координаты и скоро­сти и, следовательно, с тем большей точ­ностью можно применять к этой ча­стице понятие траектории. Таким образом, для макроскопических тел их волновые свойства не играют никакой роли. В квантовой теории рассматривается также соотношение неопределенностей для энергии Е и времени t, т. е. неопреде­ленности этих величин удовлетворяют ус­ловию DEDt³h.