Лекция 15. Элементы современной физики.

План лекции (с защитой проектов)

1 Элементы квантовой электроники. Спонтанное и вынужденное излучение. Лазеры.

2 Элементы квантовой статистики. Понятие о квантовых статистиках Бозе-Эйнштейна и Ферми-Дирака. Электропроводность металлов.

ТЕЗИСЫ

1. Квантовая статистика — раздел статисти­ческой физики, исследующий системы, ко­торые состоят из огромного числа частиц, подчиняющихся законам квантовой меха­ники. В отличие от исходных положений классической статистической физики, в ко­торой тождественные частицы различимы (частицу можно отличить от всех таких же частиц), квантовая статистика основыва­ется на принципе неразличимости тожде­ственных частиц. При этом оказывается, как будет показано ниже, что коллективы частиц с целым и полуце­лым спинами подчиняются разным стати­стикам.

Явное выражение функции распреде­ления в самом общем виде получил аме­риканский физик Д. Гиббс (1839—1903). Оно называется каноническим распре­делением Гиббса. В квантовой статисти­ке каноническое распределение Гиббса имеет вид l(E_n) =Ae^-En/(kT) (234.3), где А — постоянная, определяемая из ус­ловия нормировки к единице, n — сово­купность всех квантовых чисел, характе­ризующих данное состояние.

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе — Эйнштейна. Распределение бозо­нов по энергиям вытекает из так называе­мого большого канонического распределе­ния Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым:

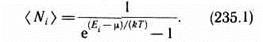
Это распределение называется распреде­лением Бозе — Эйнштейна. Здесь <Ni> — среднее число бозонов в квантовом со­стоянии с энергией E_i, k — постоянная Больцмана, Т — термодинамическая тем­пература, m — химический потенциал; m не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех <N_i> равна полному числу частиц в системе. Здесь m£0, так как иначе среднее число частиц в данном квантовом состоянии отрица­тельно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фиксированы.

Идеальный газ из фермионов — ферми-газ — описывается квантовой стати­стикой Ферми — Дирака. Распределение фермионов по энергиям имеет вид

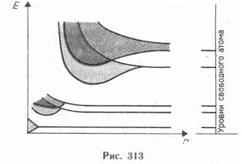
где <N_i>—среднее число фермионов в квантовом состоянии с энергией E_i, m — химический потенциал. В отличие от (235.1) m может иметь положительное значение (это не приводит к отрицатель­ным значениям чисел <N_i>). Это распреде­ление называется распределением Фер­ми — Дирака (E_i-m)/(kT). Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Для фермионов (электроны являются фермионами) среднее число частиц в кванто­вом состоянии и вероятность заселенности квантового состояния совпадают, так как квантовое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов <N(E)> =f(E), где f(E) — функция распределения электронов по состояниям. Из (236.1) следует, что при Т=0К функция распределения <N(E)³1, если E<m₀, и <N(E)³0, если E>m₀. Гра­фик этой функции приведен на рис. 312, а. В области энергий от 0 до m₀ функция <N(E)> равна единице. При E=m₀она скачкообразно изменяется до нуля. Это означает, что при Т=0К все нижние квантовые состояния, вплоть до состояния с энергией E=m₀, заполнены электронами, а все состояния с энергией, большей m₀, свободны.

Распределение Ферми — Дирака

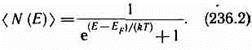
Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми. Уровню Ферми соответствует энер­гия Ферми Е_F, которую имеют электроны на этом уровне.

При температурах, отличных от 0 К, функция распределения Ферми — Дирака (236.2) плавно изменяется от 1 до 0 в узкой области (порядка kT) в окрестности Е_F (рис. 312, б). Это объясняется тем, что при T>0 небольшое число электронов с энергией, близкой к E_F, возбуждается за счет теплового движения и их энергия становится больше Е_F. Вблизи границы Ферми при E<E_F заполнение электрона­ми меньше единицы, а при E>E_F — боль­ше нуля. В тепловом движении участвует лишь небольшое число электронов, напри­мер при комнатной температуре Т » 300 К и температуре вырождения T₀=3•10⁴ К,— это 10^-5 от общего числа электронов.

Классическая теория не смогла объяснить также зависимость теплоемкости твердых тел от температуры, а квантовая стати­стика решила эту задачу. Энергия кристаллической решетки рассматривается как энергия фононного газа, подчиняющегося статистике Бозе — Эйнштейна, так как фононы являются бозонами (их спин равен нулю). Фононы могут испускаться и поглощаться, но их число не сохраняется постоянным.

Применение статистики Бозе — Эйн­штейна к фононному газу — газу из не­взаимодействующих бозе-частиц — приве­ло П. Дебая к количественному выводу, согласно которому при высоких темпера­турах, когда T>>T_D (классическая об­ласть), теплоемкость твердых тел описы­вается законом Дюлонга и Пти, а при низких температурах, когда T<<T_D (квантовая область),— пропорциональна кубу термодинамической температуры: C_V~T³. В данном случае T_D — характери­стическая температура Дебая, определяе­мая соотношением kT_D=hw_D где w_D — предельная частота упругих колебаний кристаллической решетки. Таким образом, теория Дебая объяснила расхождение опытных и теоретических (вычисленных на основе классической теории) значений теплоемкости твердых тел.

2. В основе зонной теории лежит так называемое адиабатическое приближение. Квантово-механическая система разделя­ется на тяжелые и легкие частицы — ядра и электроны. Поскольку массы и скорости этих частиц значительно различаются, можно считать, что движение электронов происходит в поле неподвижных ядер, а медленно движущиеся ядра находятся в усредненном поле всех электронов. Счи­тая, что ядра в узлах кристаллической решетки неподвижны, движение электрона рассматривается в постоянном периодиче­ском поле ядер.

Далее используется приближение са­мосогласованного поля. Взаимодействие данного электрона со всеми другими элек­тронами заменяется действием на него стационарного электрического поля, обла­дающего периодичностью кристалличе­ской решетки. Это поле создается усредненным в пространстве зарядом всех дру­гих электронов и всех ядер. Таким образом, в рамках зонной теории много­электронная задача сводится к задаче о движении одного электрона во внешнем периодическом поле — усредненном и со­гласованном поле всех ядер и электронов.

Энергия внешних электронов может принимать значения в пределах закрашен­ных на рис. 313 областей, называемых разрешенными энергетическими зонами. Каждая разрешенная зона «вмещает» в себя столько близлежащих дискретных уровней, сколько атомов содержит кристалл: чем больше в кристалле атомов, тем теснее расположены уровни в зоне. Расстояние между соседними энергетиче­скими уровнями в зоне составляет при­близительно 10^-22эВ. Так как оно столь ничтожно, то зоны можно считать практи­чески непрерывными, однако факт конечного числа уровней в зоне играет важ­ную роль для распределения электронов по состояниям.

Разрешенные энергетические зоны разделены зонами запрещенных значений энергии, называемыми запрещенными энергетическими зонами. В запрещенных зонах электроны находиться не могут.