Лекция 14. Атом и молекула водорода в квантовой теории

План лекции

1. Временное и стационарное уравнение Шредингера. Частица в одномерной прямоугольной яме. Прохождение частицы через потенциальный барьер.
2. Атом и молекула водорода в квантовой теории. Уравнение Шредингера для атома водорода.

ТЕЗИСЫ

1. Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, ограничен­ность применения классической механики к микрообъектам, диктуемая соотношени­ем неопределенностей, а также противоре­чие целого ряда экспериментов с применя­емыми в начале XX в. теориями привели к новому этапу развития квантовой тео­рии — созданию квантовой механики,описывающей законы движения и взаимо­действия микрочастиц с учетом их волно­вых свойств. Ее создание и развитие ох­ватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX в.; оно связано прежде всего с работами австрийского физика Э.Шредингера, немецкого физика В. Гейзенберга и английского фи­зика П.Дирака.

Статистическое толкование волн де Бройля и соотношение неопределенностей Гейзенберга при­вели к выводу, что уравнением движения в квантовой механике, описывающим дви­жение микрочастиц в различных силовых полях, должно быть уравнение, из которо­го бы вытекали наблюдаемые на опыте волновые свойства частиц. Основное урав­нение должно быть уравнением относи­тельно волновой функции y(х, у, z, t), так как именно она, или, точнее, величина |y|², определяет вероятность пребывания частицы в момент времени t в объеме dV, т. е. в области с координатами х и х+dх, у и y+dy, z и z+dz.

Основное уравнение нерелятивистской квантовой механики сформулировано в 1926 г. Э. Шредингером:

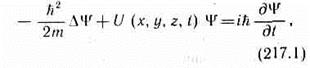
где h=h/(2p), m — масса частицы D - оператор Лапласа (Dy=д²y/дx² +д²y/дy² +д²y/дz²), i — мнимая единица, U(х, у, z, t) — потенциальная функция частицы в силовом поле, в котором она движется, y(х, у, z, t) — искомая волновая функция частицы. Уравнение справедливо для любой частицы, движущейся с малой (по срав­нению со скоростью света) скоростью, т. е. со скоростью v<<с. Оно дополняется условиями, накладываемыми на волновую функцию: 1) волновая функция должна быть конечной, однозначной и непрерывной 2) производные дy/дx, дy/дy, дy/дz, дy/дt должны быть непрерывны; 3) функция |y|² должна быть интегриру­ема; это условие в простейших случаях сводится к условию нормировки вероятно­стей. Уравнение (217.1) является общим уравнением Шредингера. Его также на­зывают уравнением Шредингера, завися­щим от времени. Для многих физических явлений, происходящих в микромире, уравнение (217.1) можно упростить, исключив зависимость yот времени, ины­ми словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии.

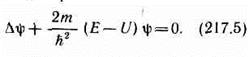
Уравнение (217.5) называется уравнением Шредингера для стационарных состояний. В это уравнение в качестве параметра входит полная энергия Е частицы. В тео­рии дифференциальных уравнений дока­зывается, что подобные уравнения имеют бесчисленное множество решений, из кото­рых посредством наложения граничных условий отбирают решения, имеющие фи­зический смысл. Для уравнения Шредин­гера такими условиями являются условия регулярности волновых функций: волно­вые функции должны быть конечными, однозначными и непрерывными вместе со своими первыми производными. Таким об­разом, реальный физический смысл имеют только такие решения, которые выража­ются регулярными функциями y . Но регу­лярные решения имеют место не при лю­бых значениях параметра Е, а лишь при определенном их наборе, характерном для данной задачи. Эти значения энергии на­зываются собственными. Решения же, ко­торые соответствуют собственным значе­ниям энергии, называются собственными функциями. Собственные значения Е мо­гут образовывать как непрерывный, так и дискретный ряд. В первом случае гово­рят о непрерывном, или сплошном, спектре, во втором — о дискретном спектре.

В квантовой механике состоя­ние микрообъекта полностью определяет­ся волновой функцией y(х, у, z, t), квад­рат модуля которой ½y(x, у, z, t)½² задает плотность вероятности нахождения части­цы в точке с координатами х, у, z. В свою очередь, волновая функция y(х, у, z, t) удовлетворяет уравнению Шредингера (217.1), содержащему пер­вую производную функции y по времени. Следо­вательно, начальное состояние y₀ есть причина, а состояние y в последующий момент — следствие. Таким об­разом, состояние системы микрочастиц, определенное в квантовой механике, однозначно вытекает из предшествующего со­стояния, как того требует принцип при­чинности.

При движении свободной частицы (U(x)=0) ее полная энергия совпадает с кине­тической. Для свободной частицы, движу­щейся вдоль оси х, уравнение Шрединге­ра (217.5) для стационарных состояний примет вид

Таким образом, свободная квантовая частица описывается плоской монохрома­тической волной де Бройля.

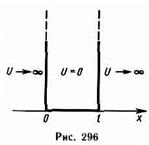
2. Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высо­кими «стенками». Такая «яма» описывает­ся потенциальной энергией вида (для про­стоты принимаем, что частица движется вдоль оси х)

где l— ширина «ямы», а энергия отсчиты­вается от ее дна (рис. 296). Уравнение Шредингера (217.5) для стационарных состояний в случае одно­мерной задачи запишется в виде

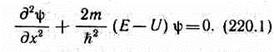
По условию задачи (бесконечно высокие «стенки»), частица не проникает за преде­лы «ямы», поэтому вероятность ее обнару­жения за пределами «ямы» равна нулю. На границах «ямы» (при х=0и х=l)непре­рывная волновая функция также должна обращаться в нуль. Следовательно, гра­ничные условия в данном случае имеют вид y(0) =y(l)=0. (220.2).

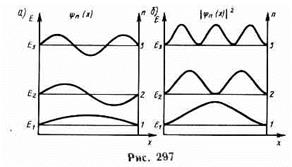
Отсюда Е_n=n²p²h²/2ml²(n=1,2,3,...) (220.7), т. е. стационарное уравнение Шредингера, описывающее движение частицы в «по­тенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях E_n, зависящих от целого числа п. Следовательно, энергия E_n частицы в «потенциальной яме» с бес­конечно высокими «стенками» принимает лишь определенные дискретные значения, т. е. квантуется. Квантованные значения энергии E_n называются уровнями энергии, а число n, определяющее энергетические уровни частицы, называется главным кван­товым числом. Таким образом, микрочасти­ца в «потенциальной яме» с бесконечно вы­сокими «стенками» может находиться толь­ко на определенном энергетическом уровне £„, или, как говорят, частица находится в квантовом состоянии п.

Графики собственных функций, соответствующие уровням энер­гии (220.7) при n=1,2,3, приведены на рис. 297, а. На рис. 297, б изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная |y_n(x)|² = y_n(x) y*_n(x) для n=1, 2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n=2 частица не может находиться в сере­дине «ямы», в то время как одинаково часто может пребывать в ее левой и пра­вой частях. Такое поведение частицы ука­зывает на то, что представления о тра­екториях частицы в квантовой механике несостоятельны. Таким образом, при­менение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высо­кими «стенками» приводит к квантован­ным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не наклады­вает.

Рассмотрим потенциальный барьер про­стейшей прямоугольной формы (рис. 298, а) для одномерного (по оси х)движения частицы.

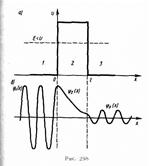
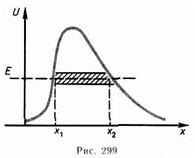
Для потенциального барьера прямоугольной формы высоты U и ширины l

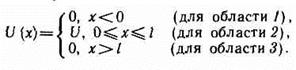
При данных условиях задачи классиче­ская частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при E>U), либо отразится от него (при Е<U) и будет двигаться в обратную сто­рону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же даже при E>U имеется отличная от нуля вероят­ность, что частица отразится от барьера и будет двигаться в обратную сторону. При E<U имеется также отличная от нуля вероятность, что частица окажется в области х>l, т.е. проникает сквозь барьер. Учитывая значение q и В₃=0, получим решения уравнения Шредингера для трех областей в следующем виде: y₁(x)=A₁e^ikx + B₁e^-ikx (для области 1), y₂(х)=А₂е^-bx+В₂e^bx (221.5) (для области 2), y₃(х)=А₃e^ikx (для области 3). В области 2 функция (221.5) уже не соответствует плоским волнам, распро­страняющимся в обе стороны, поскольку показатели степени экспонент не мнимые, а действительные. Качественный вид функций y₁(x), y₂(х) и y₃(x) показан на рис. 298, б. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же им­пульсом, т. е. с той же частотой, но с мень­шей амплитудой. Следовательно, получи­ли, что частица имеет отличную от нуля вероятность прохождения сквозь потенци­альный барьер конечной ширины. Квантовая механика приводит к специ­фическому квантовому явлению туннельного эффекта,в ре­зультате которого микрообъект может «пройти» сквозь потенциальный барьер. С классической точки зрения прохож­дение частицы сквозь потенциальный барьер при E<U невозможно, так как частица, находясь в области барьера, до­лжна была бы обладать отрицательной кинетической энергией.