Лекция 8. Тепловое излучение

План лекции:

1. Тепловое излучение. Проблемы излучения абсолютно черного тела.
2. Квантовая гипотеза и формула Планка. Фотоны. Энергия и импульс световых квантов.

ТЕЗИСЫ

1. Свечение тел, обус­ловленное нагреванием, называется тепло­вым (температурным) излучением. Тепло­вое излучение, являясь самым распростра­ненным в природе, совершается за счет энергии теплового движения атомов и мо­лекул вещества и свойственно всем телам при температуре выше О К. Тепловое излу­чение характеризуется сплошным спект­ром, положение максимума которого за­висит от температуры. При высоких темпе­ратурах излучаются короткие электромагнитные волны, при низких — длинные.

Тепловое излучение мо­жет быть равновесным. Предположим, что нагретое (излучающее) тело помещено в полость, ограниченную идеально отра­жающей оболочкой. С течением времени, в результате непрерывного обмена энер­гией между телом и излучением, наступит равновесие, т. е. тело в единицу времени будет поглощать столько же энергии, сколько и излучать. Допустим, что равно­весие между телом и излучением по какой-либо причине нарушено и тело излучает энергии больше, чем поглощает. Если в единицу времени тело больше излучает, чем поглощает (или наоборот), то темпе­ратура тела начнет понижаться (или по­вышаться). В результате будет ослаблять­ся (или возрастать) количество излучаемой телом энергии, пока, наконец, не установится равновесие. Все другие виды излучения неравновесны.

Количественной характеристикой теплового излучения служит спектральная плотность энергетической светимости (излучательности) тела—мощность излуче­ния с единицы площади поверхности тела в интервале частот единичной ширины 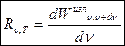или 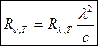Единица спектральной плотности энер­гетической светимости (R_v,T) — джоуль на метр в квадрате в секунду (Дж/м²).

Зная спектральную плотность энерге­тической светимости, можно вычислить энергетическую светимость тела 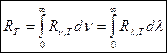. Способность тел поглощать падающее на них излучение характеризуется спек­тральной поглощательной способностью 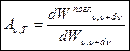, показывающей, какая доля энергии, при­носимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частота­ми от n до n+dn, поглощается телом. Спектральная поглощательная способ­ность — величина безразмерная. R_v,T и A_v,T зависят от природы тела, его термо­динамической температуры и при этом раз­личаются для излучений с различными частотами.

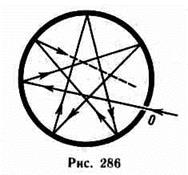
Тело, способное поглощать полностью при любой температуре все падающее на него излучение любой частоты, называется черным. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождествен­но равна единице (А^ч_v,T=1). Идеальной моделью черного тела яв­ляется замкнутая полость с небольшим отверстием О, внутренняя поверхность ко­торой зачернена (рис. 286).

Закон Кирхгофа: отношение спектральной плотности энергетической све­тимости к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и темпе­ратуры R_v,T/A_v,T=r_v,T. (198.1). Универсальная функция Кирхго­фа r_v,Tесть спектральная плотность энергетической светимости чер­ного тела. Дя всех тел отношение спек­тральной плотности энергетической свети­мости к спектральной поглощательной способности равно спектральной плотности энергетической светимости черного те­ла при той же температуре и частоте.

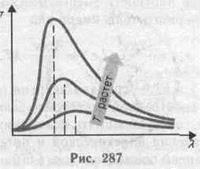
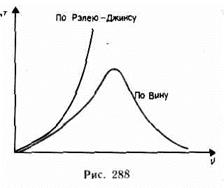
Согласно закону Стефа­на — БольцманаR_e=sT⁴ (199.1) энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры; а — постоянная Стефана — Больцмана: ее эк­спериментальное значение равно 5,67•10^-8 Вт/(м²•К⁴). Но закон не дает ответа относительно спектрального состава излучения черного тела (рис. 287). Согласно закону смещения Вина, l_max=b/Т, (199.2), т. е. длина волны l_max, соответствующая максимальному значению спектральной плотности энергетической светимости r_l,T черного тела, обратно пропорциональна его термодинамической температуре, b — постоянная Вина: ее экспериментальное значение равно 2,9•10^-3м•К. Выраже­ние (199.2) потому называют законом сме­щения Вина, что оно показывает смещение положения максимума функции r_l,T по ме­ре возрастания температуры в область коротких длин волн. Формула Рэлея — Джинсадля спек­тральной плотности энергетической свети­мости черного тела имеет вид r_v,T=(2pv²/c²)<e>=(2pv²/c²)kT, где <e>=kT — средняя энергия осцилля­тора с собственной частотой v. Как показал опыт, выражение согласуется с экспериментальными данны­ми только в области достаточно малых частот и больших температур. В области больших частот формула Рэлея — Джин­са резко расходится с экспериментом, а также с законом Вина (рис. 288). Таким образом, в рамках клас­сической физики не удалось объяснить законы распределения энергии в спектре черного тела.

2. Правильное выражение для спектральной плотности энергетической светимости чер­ного тела было найдено немецким физиком М.Планком. Согласно выдвинутой кван­товой гипотезе,атомные осцилляторы из­лучают энергию не непрерывно, а определенными порциями — квантами с энергией 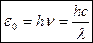, где h = 6,625•10^-34 Дж•с — постоянная Планка.Так как излучение испускается порциями, то энергия осциллятора e мо­жет принимать лишь определенные дискретные значения, кратные целому чис­лу элементарных порций энергии e₀: 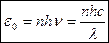, где n=0, 1, 2,.... Планк вывел для уни­версальной функции Кирхгофа формулу 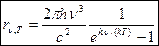. В области малых частот формула Планка совпадает с формулой Рэлея — Джинса. Из формулы Планка можно получить закон Стефана — Больцмана.

Таким образом, формула Планка позволяет получить за­кон Стефана—Больцмана. Кроме того, подстановка числовых значений дает для постоянной Стефана-Больцмана величину, хорошо согласующуюся с экспериментальными данными. Следова­тельно, формула Планка является полным решением основной задачи теплового излучения, поставленной Кирхгофом. Ее решение стало возможным лишь благода­ря революционной квантовой гипотезе Планка.