Лекция 6. Дифракция волн
План лекции:
- Дифракция волн. Принцип Гюйгенса-Френеля. Метод зон Френеля.
- Дифракция Френеля и Фраунгофера. Дифракция на одной щели и на многих щелях.
ТЕЗИСЫ
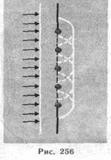
1. Дифракция - огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи препятствий от законов геометрической оптики (рис. 256). Явление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, т. е. световая волна, падающая на границу какого-либо непрозрачного тела, должна огибать его. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.
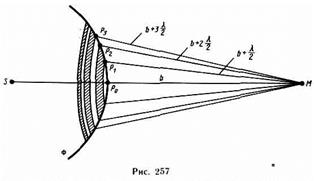
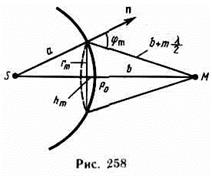
Метод зон Френеля. Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде из точечного источника S (рис. 257). Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на l/2. Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположной фазе, и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М  , где А1, А2, ..., Аm — амплитуды колебаний, возбуждаемых 1-й, 2-й, ..., m-й зонами.Для оценки амплитуд колебаний найдем площади зон Френеля (рис. 258)
, где А1, А2, ..., Аm — амплитуды колебаний, возбуждаемых 1-й, 2-й, ..., m-й зонами.Для оценки амплитуд колебаний найдем площади зон Френеля (рис. 258) 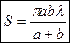 . Построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны. Действие всей волновой поверхности на точку М сводится к действию ее малого участка, меньшего центральной зоны. Радиус внешней границы m-й зоны Френеля
. Построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны. Действие всей волновой поверхности на точку М сводится к действию ее малого участка, меньшего центральной зоны. Радиус внешней границы m-й зоны Френеля 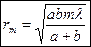 .
.
2. Рассмотрим дифракцию сферических волн, или дифракцию Френеля,осуществляемую в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.
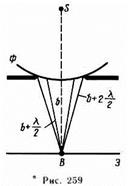
Дифракция на круглом отверстии.Сферическая волна, распространяющаяся из точечного источника 5, встречает на своем пути экран с круглым отверстием (рис. 259). Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии (если т четное, то в центре будет темное кольцо, если т нечетное — то светлое кольцо). Число зон Френеля, укладывающихся в отверстии, зависит от его диаметра.
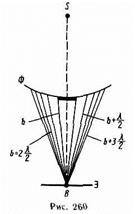
Дифракция на диске.Сферическая волна, распространяющаяся от точечного источника 5, встречает на своем пути диск (рис. 260). В точке В всегда наблюдается интерференционный максимум, соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины. С увеличением радиуса диска интенсивность центрального максимума с увеличением размеров диска уменьшается.
Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис. 261, а).
Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j, 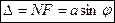 . Если число зон Френеля четное
. Если число зон Френеля четное  , (m= 1, 2, 3, ...), то в точке В наблюдается дифракционныйминимум, если же число зон Френеля нечетное
, (m= 1, 2, 3, ...), то в точке В наблюдается дифракционныйминимум, если же число зон Френеля нечетное 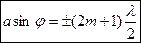 , (m=1, 2, 3, ...),то наблюдается дифракционный максимум.
, (m=1, 2, 3, ...),то наблюдается дифракционный максимум.
В точке B0 наблюдается центральный дифракционный максимум.
Направления на точки экрана, в которых амплитуда равна нулю 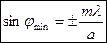 или максимальна
или максимальна 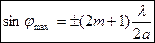 .
.
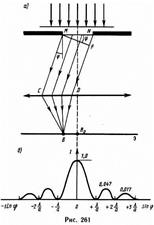
Распределение интенсивности на экране, получаемое вследствие дифракции (дифракционный спектр) (рис. 261, б). Расчеты показывают, что интенсивности центрального и последующих максимумов относятся как 1:0,047:0,017:0,0083. Сужение щели приводит к тому, что центральный максимум расплывается, а его яркость уменьшается. Положение дифракционных максимумов зависит от длины волны.
Одномерная дифракционная решетка — система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. В дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.
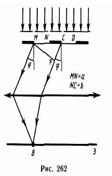
Рассмотрим дифракционную решетку (рис. 262).
Если ширина каждой щели равна a, а ширина непрозрачных участков между щелями b, то величина 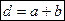 называется постоянной (периодом) дифракционной решетки,
называется постоянной (периодом) дифракционной решетки, 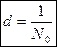 , где N0 – число щелей, приходящихся на единицу длины решетки.
, где N0 – число щелей, приходящихся на единицу длины решетки.
Полная дифракционная картина для двух щелей определяется из условия:
1) главные минимумы 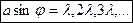
2) дополнительные минимумы 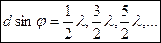
3) главные максимумы 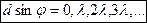
Число главных максимумов 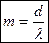
Дата добавления: 2015-10-13; просмотров: 1068;
