ЛЕКЦИЯ 5. Интерференция светОВЫХ ВОЛН.

План лекции:

1. Свойства световых волн. Волновой пакет. Групповая скорость.
2. Интерференция световых волн. Когерентность.

тезисы лекции

1. Геометрическое место точек, до которых доходят колебания к мо­менту времени t, называется волновым фронтом. Геометрическое место точек, ко­леблющихся в одинаковой фазе, называет­ся волновой поверхностью. В принципе волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Со­ответственно волна называется плоской или сферической. Бегущими волнами называются волны, ко­торые переносят в пространстве энергию. Перенос энергии в волнах количественно характеризуется вектором плотности по­тока энергии. Этот вектор для упругих волн называется вектором Умова. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, пере­носимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распро­странения волны.

Уравнение колебаний частиц, лежащих в плоскости х, имеет вид 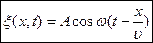, откуда следует, что x(х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Это уравнение есть уравнение бегу­щей волны. Если плоская волна распро­страняется в противоположном направлении, то в формуле будет знак +.

В общем случае уравнение плоской волны, распространяющейся вдоль поло­жительного направления оси х в среде, не поглощающей энергию, имеет вид 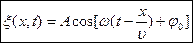, где А = const — амплитуда волны, w — циклическая частота волны, j₀ — началь­ная фаза колебаний, определяемая в об­щем случае выбором начал отсчета х и t, [w(t-x/v)+j₀]—фаза плоской волны. Для характеристики волн использует­ся волновое число 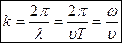Тогда уравнение волны можно записать в виде 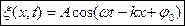Скорость v распростране­ния волны есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью.

Урав­нение сферической волны — волны, волновые поверхности которой имеют вид кон­центрических сфер, записывается как , где r — расстояние от центра волны до рассматриваемой точки среды. Отсюда фазовая скорость . Если фазовая скорость волн в среде за­висит от их частоты, то это явление на­зывают дисперсией волн, а среда, в кото­рой наблюдается дисперсия волн, называ­ется диспергирующей средой.

Распространение волн в однородной изотропной среде в общем случае описы­вается волновым уравнением — диффе­ренциальным уравнением в частных про­изводных 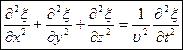, где v — фазовая скорость. Для плоской волны волновое уравнение имеет вид 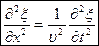. Если среда, в которой распространяется одновременно несколько волн, линейна, т. е. ее свойства не изменяются под дей­ствием возмущений, создаваемых волной, то к ним применим принцип суперпозиции волн: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирую­щее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают части­цы, участвуя в каждом из слагающих во­лновых процессов. Вол­новым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый мо­мент времени ограниченную область про­странства. Групповая скорость - скорость движения группы волн, образующих в каждый мо­мент времени локализованный в простран­стве волновой пакет.

2. При наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспре­деление светового потока, в результате чего в одних местах возникают максиму­мы, а в других — минимумы интенсивно­сти. Это явление называется интерферен­цией света. Необходимым условием интер­ференции волн является их когерентность, т. е. согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. Этому условию удовлетворяют монохроматические во­лны — неограниченные в пространстве волны одной определенной и строго по­стоянной частоты. Так как ни один реаль­ный источник не дает строго монохромати­ческого света, то волны, излучаемые лю­быми независимыми источниками света, всегда некогерентны.

Прерывистое излуче­ние света атомами в виде отдельных ко­ротких импульсов называется волновым цугом. Любой немонохроматический свет можно представить в виде совокупности сменяющих друг друга независимых гар­монических цугов. Средняя продолжитель­ность одного цуга t_ког называется време­нем когерентности. Когерентность су­ществует только в пределах одного цуга, и время когерентности не может превы­шать время излучения, т. е. t_ког<t. При­бор обнаружит четкую интерференцион­ную картину лишь тогда, когда время раз­решения прибора значительно меньше времени когерентности накладываемых световых волн.

Если волна распространяется в одно­родной среде, то фаза колебаний в опреде­ленной точке пространства сохраняется только в течение времени когерентности t_ког. За это время волна распространяется в вакууме на расстояние l_ког=сt_ког, на­зываемое длиной когерентности(или дли­ной цуга). Таким образом, длина коге­рентности есть расстояние, при прохожде­нии которого две или несколько волн утрачивают когерентность. Отсюда следу­ет, что наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света. Когерент­ность колебаний, которые совершаются в одной и той же точке пространства, опре­деляемая степенью монохроматичности волн, называется временной когерент­ностью.

Радиусом когерентности (или длиной пространствен­ной когерентности) называется макси­мальное поперечное направлению распро­странения волны расстояние, на котором возможно проявление интерференции. Та­ким образом, пространственная когерен­тность определяется радиусом когерен­тности. Радиус когерентности r_ког~l/j, где l — длина световых волн, j — угловой размер источника. Для получения когерент­ных световых волн применяют метод раз­деления волны, излучаемой одним источ­ником, на две части, которые после про­хождения разных оптических путей на­кладываются друг на друга и наблюдается интерференционная картина.

Разность фаз колебаний, возбуждаемых волнами в точке М, 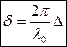Произведение геометрической длины s пути световой во­лны в данной среде на показатель n пре­ломления этой среды называется оптиче­ской длиной пути L, а D=L₂-L₁— раз­ность оптических длин проходимых во­лнами путей — называется оптической разностью хода.

Условие интерферен­ционного максимума: если 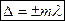(m=0, 1, 2,...), то 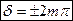и колебания, возбуждаемые в точке М обеими волнами, будут про­исходить в одинаковой фазе.

Условие интерферен­ционного минимума: если (m = 0,1,2,…), то 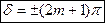и колебания, возбуж­даемые в точке М обеими волнами, будут происходить в противофазе.

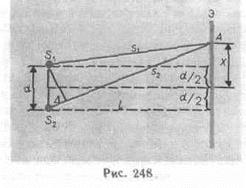
Расстояние между двумя соседними максимумами (или минимумами), называ­емое шириной интерференционной полосы (рис. 248), равно .