Лекция 3 Электромагнитные колебания и волны
СПЕЦИАЛЬНОСТИ: 5В071200, 5В072400, 5В070800, 5В073100, 5В073200
ТЕЗИСЫ ЛЕКЦИЙ
МОДУЛЬ 1 ЭЛЕКТРОМАГНЕТИЗМ. ОПТИКА
Лекция 2 Явление электромагнитной индукции
План лекции
1. Основной закон электромагнитной индукции. Правило Ленца. Явление взаимо- и самоиндукции. Индуктивность. Энергия и плотность магнит. поля.
2.Ток смещения. Система уравнений Максвелла. Волновое уравнение. Скорость распространения электромагнитного возмущения.
Тезисы
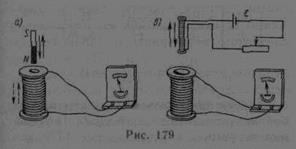
1. Явление электромагнитной индукции (опыты Фарадея) (рис. 179). Если происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; возникновение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции.ЭДС выражается в вольтах (В).
Закон Фарадея ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром 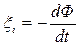 . Знак минус в формуле является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока. Циркуляция вектора ЕВ этого поля по любому неподвижному контуру проводника представляет собой э.д.с. электромагнитной индукции
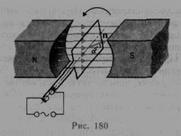
. Знак минус в формуле является математическим выражением правила Ленца — общего правила для нахождения направления индукционного тока. Циркуляция вектора ЕВ этого поля по любому неподвижному контуру проводника представляет собой э.д.с. электромагнитной индукции 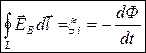 . Если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная э.д.с., изменяющаяся по гармоническому закону.
. Если в однородном магнитном поле равномерно вращается рамка, то в ней возникает переменная э.д.с., изменяющаяся по гармоническому закону.
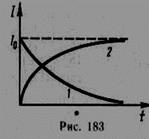
Индуктивность – это физическая величина, характеризующая магнитные свойства электрической цепи. Индуктивность контура определяется магнитным потоком, сцепленным с контуром, когда ток, создающий этот поток, равен единице 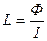 . Индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. Единица индуктивности - генри(Гн): 1 Гн=1 Вб/А=1В•с/А. Индуктивность соленоида
. Индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. Единица индуктивности - генри(Гн): 1 Гн=1 Вб/А=1В•с/А. Индуктивность соленоида 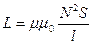 . Из закона Фарадея следует, что любое изменение сцепленного с контуром потока магнитной индукции приводит к возникновению электродвижущей силы индукции и вследствие этого появляется индукционный ток. Работа по созданию магнитного потока Ф
. Из закона Фарадея следует, что любое изменение сцепленного с контуром потока магнитной индукции приводит к возникновению электродвижущей силы индукции и вследствие этого появляется индукционный ток. Работа по созданию магнитного потока Ф 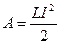 . Энергия магнитного поля
. Энергия магнитного поля 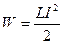 .Однородное магнитное поле внутри длинного соленоида
.Однородное магнитное поле внутри длинного соленоида 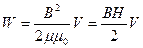 . Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью
. Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью 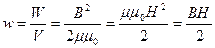
2. Гипотеза Максвелла: всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре. По Максвеллу, изменяющееся во времени магнитное поле порождает электрическое поле ЕB, циркуляция которого 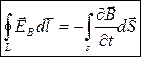 , где символ частной производной подчеркивает тот факт, что интеграл
, где символ частной производной подчеркивает тот факт, что интеграл 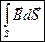 является функцией только от времени. Сравнение циркуляции векторов напряженности электростатического поля (обозначим его eq) вдоль любого замкнутого контура равна нулю
является функцией только от времени. Сравнение циркуляции векторов напряженности электростатического поля (обозначим его eq) вдоль любого замкнутого контура равна нулю 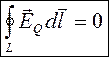 . Следовательно, электрическое поле ЕB, возбуждаемое магнитным полем, как и само магнитное поле, является вихревым.
. Следовательно, электрическое поле ЕB, возбуждаемое магнитным полем, как и само магнитное поле, является вихревым.
Идея о симметрии во взаимозависимости электрического и магнитного полей Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Ток смещения введен Максвеллом для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем.
Плотность тока смещения 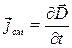 Ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле (линии индукции магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на рис. 197 штриховой линией). В диэлектриках ток смещения состоит из двух слагаемых. Плотность тока смещения в диэлектрике
Ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле (линии индукции магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на рис. 197 штриховой линией). В диэлектриках ток смещения состоит из двух слагаемых. Плотность тока смещения в диэлектрике 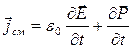 можно получить, если продифференцировать формулу для электрического смещения
можно получить, если продифференцировать формулу для электрического смещения 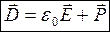 . Плотность тока поляризации
. Плотность тока поляризации 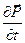 обусловлена упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах). Возбуждение магнитного поля токами поляризации правомерно, т.к. токи поляризации по своей природе не отличаются от токов проводимости.
обусловлена упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах). Возбуждение магнитного поля токами поляризации правомерно, т.к. токи поляризации по своей природе не отличаются от токов проводимости.
По Максвеллу, полный ток всегда замкнут, т.е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости 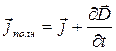 Полный ток - поток вектора плотности полного тока
Полный ток - поток вектора плотности полного тока 
Теорема о циркуляции вектора Н (циркуляция вектора Н по произвольному замкнутому контуру равна алгебраической сумме токов проводимости, охватываемых данным контуром) 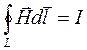 Обобщенная теорема о циркуляции вектора Н
Обобщенная теорема о циркуляции вектора Н 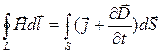 .
.
Полная система уравнений Максвелла в интегральной форме
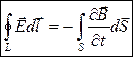 (1)
(1) 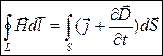 (2)
(2) 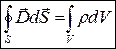 (3)
(3) 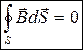 (4)
(4)
Электрическое поле может быть как потенциальным (eq), так и вихревым (ЕB), поэтому напряженность суммарного поля Е=ЕQ+ЕB. Уравнение (1) показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля. Обобщенная теорема о циркуляции вектора Н (уравнение 2) показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями. Уравнение (3) – это теорема Гаусса для поля D, если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r. Уравнение (4) – это теорема Гаусса для поля В.Величины, входящие в уравнения Максвелла, не являются независимыми, и между ними существует следующая связь (изотропные, не сегнетоэлектрические и не ферромагнитные среды): 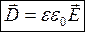 (5)
(5)  (6)
(6) 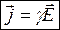 (7) где e0 и m0 — электрическая и магнитная постоянные, e и m— диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества. Уравнения Максвелла для стационарных полей (когда
(7) где e0 и m0 — электрическая и магнитная постоянные, e и m— диэлектрическая и магнитная проницаемости, g — удельная проводимость вещества. Уравнения Максвелла для стационарных полей (когда 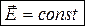 (8)
(8) 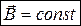 (9))
(9)) 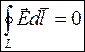 (10)
(10) 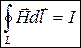 (11)
(11) 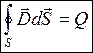 (12)
(12) 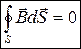 (13) т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости.
(13) т. е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного — только токи проводимости.
Теория Максвелла, являясь обобщением основных законов электрических и магнитных явлений, смогла объяснить не только уже известные экспериментальные факты, что также является важным ее следствием, но и предсказала новые явления. Одним из важных выводов этой теории явилось существование магнитного поля токов смещения, что позволило Максвеллу предсказать существование электромагнитных волн— переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью.
Лекция 3 Электромагнитные колебания и волны
1. Свободные и вынужденные электромагнитные колебания. Переменный электрический ток. Закон Ома для переменного тока
2. Волновое уравнение для электромагнитного поля. Свойства электромагнитных волн. Плотность потока электромагнитной энергии. Вектор Умова-Пойтинга. Излучение диполя.
Тезисы
1. Свободные затухающие колебания — колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается. Закон затухающих колебаний определяется свойствами колебательных систем. Закон Ома для контура RLC 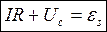
 , где
, где 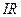 - напряжение на резисторе. Дифференциальное уравнение свободных затухающих колебанийзаряда в контуре
- напряжение на резисторе. Дифференциальное уравнение свободных затухающих колебанийзаряда в контуре 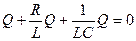 или
или 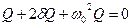 , где
, где 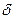 - коэффициент затухания, равный
- коэффициент затухания, равный  . Его решение
. Его решение 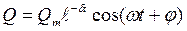 . Затухающие колебания не являются периодическими (рис. 208).
. Затухающие колебания не являются периодическими (рис. 208).
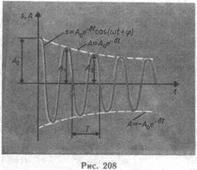

Амплитуда затухающих колебаний 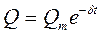 . Циклическая частота
. Циклическая частота 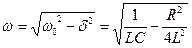 , период
, период 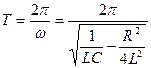 . Характеристиками колебательных систем являются декремент затухания, время релаксации, логарифмический декремент затухания, добротность системы.
. Характеристиками колебательных систем являются декремент затухания, время релаксации, логарифмический декремент затухания, добротность системы.
Если A(t) и A(t+T)— амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение 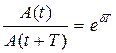 называется декрементом затухания, а его логарифм
называется декрементом затухания, а его логарифм 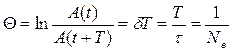 — логарифмическим декрементом затухания; Ne — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации
— логарифмическим декрементом затухания; Ne — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Промежуток времени, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации 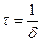 . Добротность колебательной системы
. Добротность колебательной системы 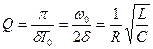 Электрический резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешней ЭДС к частоте, равной или близкой собственной частоте колебательного контура. Зависимость амплитуды колебаний заряда на конденсаторе от частоты
Электрический резонанс – явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешней ЭДС к частоте, равной или близкой собственной частоте колебательного контура. Зависимость амплитуды колебаний заряда на конденсаторе от частоты 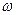 внешней ЭДС
внешней ЭДС 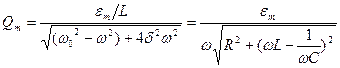 , где
, где  ,
,  . Резонансная частота – частота, при которой амплитуда достигает максимального значения
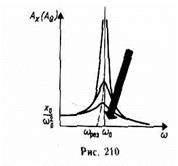
. Резонансная частота – частота, при которой амплитуда достигает максимального значения 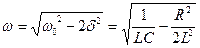 . Зависимость амплитуды заряда на конденсаторе от частоты внешней ЭДС при различных коэффициентах затухания (рис. 210). При
. Зависимость амплитуды заряда на конденсаторе от частоты внешней ЭДС при различных коэффициентах затухания (рис. 210). При 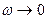 все кривые достигают статического отклонения
все кривые достигают статического отклонения 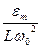 , а при
, а при 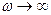 - асимптотически стремятся к нулю. Чем больше
- асимптотически стремятся к нулю. Чем больше 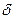 , тем ниже и левее максимумы резонансных кривых.
, тем ниже и левее максимумы резонансных кривых.
2. Сила тока при установившихся вынужденных колебаниях 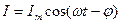 , где
, где 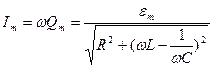 амплитуда тока,
амплитуда тока, 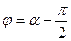 - сдвиг по фазе между током и внешней ЭДС. Резонансная частота для силы тока
- сдвиг по фазе между током и внешней ЭДС. Резонансная частота для силы тока 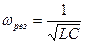 . Резонансные кривые для амплитуды силы тока - рис. 211. Амплитуда силы тока максимальна при
. Резонансные кривые для амплитуды силы тока - рис. 211. Амплитуда силы тока максимальна при 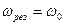 и равна
и равна 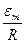 . Чем больше коэффициент затухания
. Чем больше коэффициент затухания 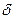 , тем ниже максимум.
, тем ниже максимум.
Электрический ток, величина и направление которого изменяются во времени, есть переменный ток. Установившиеся электромагнитные вынужденные колебания можно рассматривать как протекание переменного тока в цепи. Цепь переменного тока - цепь, содержащая резистор, катушку индуктивности и конденсатор, к которому приложено переменное напряжение.
1.Переменный ток, текущий через резистор сопротивлением R (L®0, С®0). При выполнении условия квазистационарности ток через резистор определяется законом Ома: 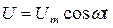
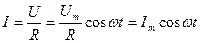
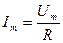 - амплитуда силы тока)
- амплитуда силы тока)
2. Переменный ток, текущий через конденсатор. Падение напряжения на конденсаторе 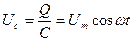 . Сила тока
. Сила тока  , где амплитуда силы тока
, где амплитуда силы тока 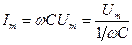 , а величина
, а величина 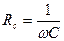 есть реактивное емкостное сопротивление. Для постоянного тока RC=¥, он через конденсатор течь не может. Падение напряжения на конденсаторе
есть реактивное емкостное сопротивление. Для постоянного тока RC=¥, он через конденсатор течь не может. Падение напряжения на конденсаторе 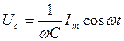 Падение напряжения UC отстает по фазе от текущего через конденсатор тока I на p/2.
Падение напряжения UC отстает по фазе от текущего через конденсатор тока I на p/2.
3.Переменный ток, текущий через катушку. ЭДС самоиндукции 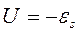 . Закон Ома
. Закон Ома 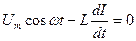 Падение напряжения на катушке
Падение напряжения на катушке 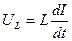 Сила тока
Сила тока 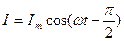 , где
, где 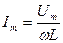 - амплитудное значение силы тока,
- амплитудное значение силы тока, 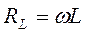 - реактивное индуктивное сопротивление. Падение напряжения на катушке
- реактивное индуктивное сопротивление. Падение напряжения на катушке 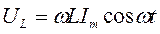 . Для постоянного тока катушка не имеет сопротивления. Падение напряжения UL опережает по фазе ток I, текущий через катушку, на p/2. Для активного сопротивления
. Для постоянного тока катушка не имеет сопротивления. Падение напряжения UL опережает по фазе ток I, текущий через катушку, на p/2. Для активного сопротивления 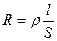 – график
– график 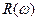 есть прямая, параллельная оси
есть прямая, параллельная оси 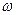 , для индуктивного сопротивления
, для индуктивного сопротивления 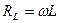 - график
- график 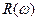 есть прямая пропорциональность, для емкостного сопротивления
есть прямая пропорциональность, для емкостного сопротивления 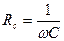 - график
- график 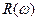 есть обратная пропорциональность. Условие резонанса
есть обратная пропорциональность. Условие резонанса 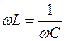 ,
, 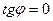 ,
, 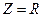 Резонансная частота
Резонансная частота 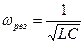 Средняя мощность
Средняя мощность 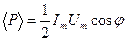 ,
, 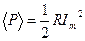 .Действующее значение тока
.Действующее значение тока 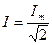 и напряжения
и напряжения 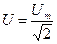 Средняя мощность
Средняя мощность 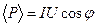 , коэффициент мощности
, коэффициент мощности 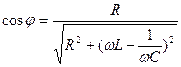
1. Одним из важнейших следствий уравнений Максвелла является существование электромагнитных волн. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению:
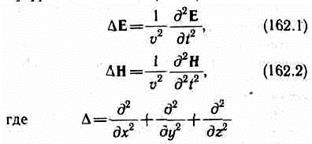
— оператор Лапласа, v — фазовая скорость.
Всякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением
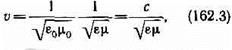
где с= 1/Öe0m0, e0 и m0 — соответственно электрическая и магнитная постоянные, e и m — соответственно электрическая и магнитная проницаемости среды.
В вакууме (при e=1 и m=1) скорость распространения электромагнитных волн совпадает со скоростью с. Так как em>1, то скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.
При вычислении скорости распространения электромагнитного поля по формуле (162.3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость e и m, от частоты. Совпадение же размерного коэффициента в (162.3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представляет собой электромагнитные волны.
Следствием теории Максвелла является поперечность электромагнитных волн: векторы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору v скорости распространения волны, причем векторы Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне векторы Е и Н всегда колеблются в одинаковых фазах, причем мгновенные значения £ и Я в любой точке связаны соотношением Öe0e=Öm0mН. Следовательно, E и H одновременно достигают максимума, одновременно обращаются в нуль и т. д. От волновых уравнений можно перейти к уравнениям
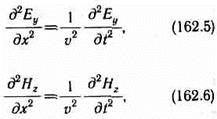
где соответственно индексы у и z при Е н Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей у и z.
Уравнениям удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями
Еу=Е0cos(wt-kx+j), (162.7)
Hz= H0cos(wt-kx+j),(162.8)
где е0и Н0 — соответственно амплитуды напряженностей электрического и магнитного полей волны, w — круговая частота волны, k=w/v— волновое число, j— начальные фазы колебаний в точках с координатой х=0. В уравнениях (162.7) и (162.8) j одинаково, так как колебания электрического и магнитного векторов в электромагнитной волне происходят с одинаковой фазой.
Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей wэл и wм электрического и магнитного полей.Получим, что плотность энергии электрического и магнитного полей в каждый момент времени одинакова, т. е. wэл = wм.
Умножив плотность энергии w на скорость v распространения волны в среде, получим модуль плотности потока энергии: S=EH. Так как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ЕН] совпадает с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова-Пойнтинга:
S = [EH]. Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.
Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Г. Герца), то из теории Максвелла следует, что электромагнитные волны должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца. Однако значение этого давления ничтожно. Можно оценить, что при средней мощности солнечного излучения, приходящего на Землю, давление для абсолютно поглощающей поверхности составляет примерно 5 мкПа. В исключительно тонких экспериментах, ставших классическими, П. Н. Лебедев в 1899 г. доказал существование светового давления на твердые тела, а в 1910 г. - на газы. Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны.
Существование давления электромагнитных волн приводит к выводу о том, что электромагнитному полю присущ механический импульс. Импульс электромагнитного поля p=W/c, где W — энергия электромагнитного поля. Выражая импульс как р=mc (поле в вакууме распространяется со скоростью с), получим p = mc=W/c, откуда W = mc2
Это соотношение между массой и энергией свободного электромагнитного поля является универсальным законом природы. Согласно специальной теории относительности, выражение имеет общее значение и справедливо для любых тел независимо от их внутреннего строения.
3. Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону р = р0coswt, где р0 — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда +Q и отрицательного заряда -Q, гармонически колеблющегося вдоль направления р с частотой w.
Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему можно рассчитывать рассматривая излучение диполя. Если волна распространяется в однородной изотропной среде, то время прохождения волны до точек, удаленных от диполя на расстояние r, одинаково. Поэтому во всех точках сферы, центр которой совпадает с диполем, фаза колебаний одинакова, т. е. в волновой зоне волновой фронт будет сферическим и, следовательно, волна, излучаемая диполем, есть сферическая волна. Диполь сильнее всего излучает в направлениях, перпендикулярных его оси (q=p/2). Вдоль своей оси (q=0 и q=p) диполь не излучает вообще. Диаграмма направленности излучения диполя позволяет формировать излучение с определенными характеристиками и используется при конструировании антенн.
Дата добавления: 2015-10-13; просмотров: 2019;
