Дифференциальные уравнения первого порядка с разделяющимися переменными.

Определение 7.Уравнение вида 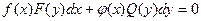называется уравнением с разделяющимися переменными.

Это уравнение можно привести к виду 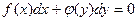, разделив все члены уравнения на произведение .

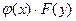Например, решить уравнение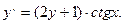

Решение. Производная равна 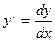, значит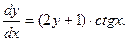

Разделяя переменные, получим:

.

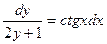Теперь интегрируем:

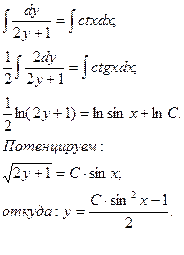
Решите дифференциальное уравнение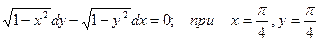

Решение. Это уравнение первого порядка с разделяющимися переменными. Для разделения переменных этого уравнения в виде 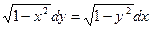и разделим его почленно на произведение 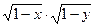. В результате получим 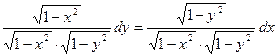или

интегрируя обе части последнего уравнения, получим общее решение

аrcsin y =arcsin x + C

Найдем теперь частное решение, удовлетворяющее начальным условиям 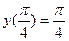. Подставляя в общее решение начальные условия, получим

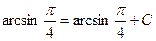; откуда C=0

Следовательно, частное решение имеет вид arc sin y=arc sin x, но синусы равных дуг равны между собой

sin (arc sin y)=sin (arc sin x).

Откуда, по определению арксинуса, следует, что y=x.