Дифференциальные уравнения первого порядка с разделёнными переменными

Определение 6. Уравнение вида

f(x)dx + φ(y)dy = 0,

где f(x) и φ(y) – данные функции, называется уравнением с разделёнными переменными.

Это уравнение переписывают в виде:

f(x)dx = – φ(y)dy

и рассматривают как равенство двух дифференциалов. Решение таких уравнений выполняется непосредственным интегрированием.

Посмотрим на конкретных примерах.

Решить уравнения:

1) xdx + ydy = 0;

2) ;

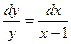3) y ^,= x;

4) Найти частные решения дифференциального уравнения: dy = (x²-1), если y = 4 при x = 1.

Решение.

1 xdx + ydy = 0,

ydy = – xdx,

∫ydy = – ∫xdx,

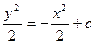– общее решение.

2 ,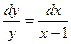

,

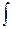
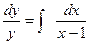lny = ln(x-1) + lnc,

lny = lnc(x-1),

y = c(x-1) – общее решение.

3 y^, = x,

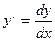, следовательно,

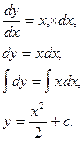
4 Найти частные решения дифференциального уравнения: dy = (x²-1), если y = 4 при x = 1.

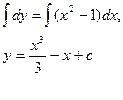
То есть нашли сначала общее решение данного уравнения. Теперь начинаем использовать начальные условия, вместо y подставляем 4, а вместо x –1.

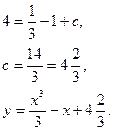
Задача нахождения частного решения по конкретным начальным условиям называется задачей Коши.