Функция называется непрерывной на отрезке , если она непрерывна в каждой точке этого отрезка.

Исследуем на непрерывность функцию .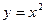

Решение. Пусть приращение аргумента х равно Δх, тогда функция y получит какое-то приращение Δy. Имеем

,

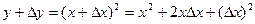откуда

.

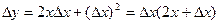Очевидно, что при любом фиксированном значении х и при Δх, стремящемся к нулю, Δy также стремится к нулю, то есть функция 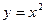непрерывна при любом значении х.

Вопросы для повторения

1 Сформулируйте определение функции.

2 Что называется областью определения функции?

3 Что называется областью значения функции?

4 Какими способами может быть задана функция?

5 Какие функции называются чётными?

6 Какие функции называются нечётными?

7 Какие функции называются возрастающими?

8 Какие функции называются убывающими?

9 Дайте определение предела функции.

10 Перечислите свойства пределов.

11 Перечислите виды неопределённостей.

12 Запишите первый и второй замечательный пределы.

13 Дайте определение функции непрерывной в точке и на отрезке.