Ускорение. Движение точки по кругу.
Лекция № 1
Тема 1.1.1 Введение. Классическая механика. Основные кинематические величины: перемещение, скорость,
ускорение. Движение точки по кругу.
План
1Предмет физики и общие методы научного познания.
2Механика. Основные понятия и величины.
3Перемещение. Скорость.
4Ускорение.
5Движение точки по криволинейной траектории.
Литература:
[1] Чолпан П.П. Фізика: Підручник. – К.: Вища шк., 2004. – 567 с.
(стор.3, 39-44)
1В древности физикой называли учение о природе (от греч. φνσιχά – природа).
Систематизация нагроможденных знаний о природных явлениях со временем привело к возникновению науки. Знания о природе расширялись и уточнялись благодаря наблюдениям, а на более высокой стадии науки – экспериментам.
Физика изучает простейшие и наиболее общие свойства материи и формы ее движения (механические, тепловые, электромагнитные и т.д.), которые относятся к высшим, более сложным формам движения (химическим, биологическим и др.).
Современная физика изучает разные физические поля, элементарные частицы, ионы, атомы, молекулы и их соединения. Молекулы и атомы изучают также химия и биология. Так, на основании общности объекта исследования происходит взаимное проникновение наук. Применение физических методов исследования в химии, биологии, геологии, астрономии приводит к интеграции науки, возникновению новых самостоятельных наук – физической химии, биофизики, геофизики, астрофизики и т.д.
С развитием физики уточняются и усовершенствуются ее законы и понятия, изменяются физические теории. При этом изменяется и предмет физики, и методы физического исследования природы.
Современная физика, которая экспериментальными методами, теоретическими обобщениями и предвидением изучает простые, но наиболее общие свойства и объективные пространственно-временные законы движения материи, количественные и качественные изменения ее, связанные со строением, взаимодействием и превращением всех ее видов и состояний, является частью природоведения.
2 Механика – это наука о простейшей форме движения тел (механическом движении или перемещении). Движение в широком философском понимании – это изменение вообще, какое-либо изменение или процесс: физический, химический, биологический и т.д.
Под механическим движением понимают изменение положения тела со временем относительно другого тела или системы тел, которые условно считают неподвижными. Такую систему тел вместе с часами называют системой отсчета.
Тело, деформациями которого в условиях решения задачи можно пренебречь, называют абсолютно твердым.
Тело, размерами которого в условиях определенной задачи можно пренебречь, называют материальной точкой.
Поступательное движение – это такое движение, при котором какая-либо прямая, проведенная в теле, которое движется, остается параллельной сама себе.
При вращательном движении все точки тела движутся по кругам, центры которых лежат на одной прямой, называемой осью вращения. Ось вращения может быть вне тела.
Линию, описываемую во время движения материальной точкой, называют траекторией. По форме траектории движения делят на прямолинейное и криволинейное. Расстояние, которое отсчитано вдоль траектории, называют пройденным путем.
Механику делят на три раздела: кинематику, статику и динамику. Кинематика изучает движение тел без учета причин, обусловливающих это движение. Статика рассматривает условия равновесия тел. Динамика изучает движение тел в связи с теми причинами (взаимодействие между телами), которые порождают тот или иной характер движения. Поскольку равновесие – отдельный случай движения, законы статики вытекают из законов динамики.
3 Положение материальной точки в пространстве можно задать с помощью радиус-вектора 
. Зафиксируем определенный момент времени t. Ему отвечает значение 
радиус-вектора. В течение следующего (после момента t) небольшого промежутка времени Δt (будем называть его элементарным) точка проходит элементарный путь и совершает элементарное перемещение Δ , которое совпадает с приростом радиус-вектора за время Δt.
Скоростью называют границу, к которой стремится отношение Δ /Δt при неограниченном уменьшении Δt. Скорость можно определить как производную от радиус-вектора точки, которая движется, по времени:
.
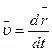Как вытекает из определения, скорость – величина векторная. Вектор скорости имеет направление, совпадающее с направлением касательной к траектории в определенной точке.
Соответственно формуле, модуль вектора скорости запишем так:
.
Для модуля скорости получим
.
Скорость выражается в метрах в секунду (СИ) и сантиметрах в секунду (СГС).
4 Производную скорости материальной точки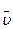 
со временем t характеризуют ускорением
.
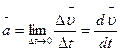Если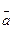 
совпадает по направлению с 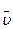, то скорость увеличивается, и движение будет ускоренным. Если 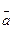противоположно по направлению к 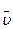, то скорость уменьшается, и движение будет замедленным.
При равнопеременном прямолинейном движении справедлива формула =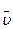 
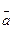+ t,
где 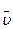– скорость в момент времени; – скорость в начальный момент времени (при t=0); 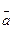– ускорение. При этом векторы 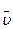, , 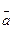направлены вдоль прямой в одну сторону, если скорость по величине со временем увеличивается и противоположно, если скорость уменьшается.
5 Определим ускорение точки в случае ее движения по криволинейной траектории. Пусть в момент времени t точка была в положении А, а в момент времени t+Δt – в положении В. Скорост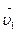и 
и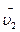 
в точках А и В направлены по касательным к траектории в этих точках. перенесем вектор 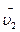в точку А. Изменение скорости за промежуток времени Δt определяется вектором Δ 
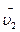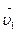= - . Из рисунка видим, что
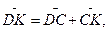или 
. Тогда ускорение в точке А запишем так:
.
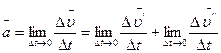Вектор аn =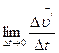 
называют нормальным ускорением, а вектор 
= 
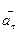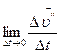– тангенциальным. Ускорение 
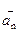перпендикулярно вектору скорости 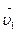и всегда направлено к центру кривизны. Отсюда и название этого вектора – нормальный (то есть перпендикулярный).
Модуль нормального ускорения можно записать так аn=υ2/R.
Соответственно тангенциальное ускорение 
, или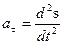 
.
Вектор 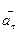показывает, как изменяется скорость по численному значению, а вектор 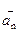характеризует изменение скорости по направлению. Итак, для полного ускорения запишем:
.
Контрольные вопросы
1 Что изучает физика?
2 Какие физические методы научного познания вы знаете?
3 Назовите основные кинематические величины, дайте их определение.
Содержательный модуль 1.1 Кинематика и динамика поступательного и вращательного движений твердого тела
Тема 1.1.2: Законы Ньютона. Закон сохранения импульса.(Самостоятельное изучение)
План
- Первый закон Ньютона. Инертность. Инерциальные системы отсчета.
- Масса тела.
- Сила.
- Второй закон Ньютона.
- Импульс тела. Другая запись второго закона Ньютона.
- Принцип независимости действия силы.
- Третий закон Ньютона.
- Закон сохранения импульса.
Литература:
[1] Чолпан П.П. Фізика: Підручник. – К.: Вища шк., 2004. – 567 с.
(стор.51, 55,59,60)
1В основе динамики, которая рассматривает законы движения тел и те причини, которые его вызывают или изменяют, лежат законы Ньютона.
Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока действие со стороны других тел не вынудит ее изменить это состояние.
Первый закон Ньютона называют законом инерции, а свойство тел сохранять состояние покоя или равномерного прямолинейного движения без действия на них других тел называют инертностью.
Системы отсчета, относительно которых выполняется первый закон Ньютона, называются инерциальными системами отсчета. Содержание первого закона Ньютона сводится к двум утверждениям:
1) всем телам свойственна инертность;
2) существуют инерциальные системы отсчета.
Инерциальных систем существует бесконечное множество. Произвольная система отсчета, которая движется относительно некоторой инерциальной системы прямолинейно и равномерно, будет также инерциальной.
Инерциальной системой отсчета можно считать систему отсчета, связанную с Солнцем, – начало координат находится в центре Солнца, а оси проведены в направлении определенных звезд. Система отсчета, которая связана с Землей, строго говоря, неинерциальная.
Но в основном в практических задачах эффекты, которые обусловлены неинерциальностью земной системы отсчета, очень малы. Поэтому в дальнейшем будем считать эту систему отсчета инерциальной.
2 Физическая величина, которая является мерой инертности материальной точки, называется инертной массой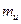 
. Масса тела тоже характеризует способность его взаимодействовать с другими телами согласно закону всемирного тяготения. В этом случае масса является мерой гравитационного взаимодействия и называется гравитационной массой 
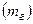. В современной физике с высокой степенью точности установлено, что 
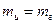, если скорость материальной точки намного меньше скорости света в вакууме.
Масса тела – скалярная величина и, как показывает опыт, масса – величина аддитивная: масса тела равна сумме масс всех частей этого тела. Соответственно масса произвольной механической системы равна сумме масс всех материальных точек, на которые эту систему можно мысленно разбить.
Чтобы измерить массу тела, нужно сравнить ее с эталоном, принятым за единицу массы. В повседневной практике сравнивают массы тел на рычажных весах.
3 Важнейшей характеристикой взаимодействия тел является сила.
Силой называется векторная величина, которая является мерой механического действия на тело со стороны других тел, вследствие которого тело получает ускорение или изменяет свою форму и размеры.
В каждый момент времени сила характеризуется численным значением, направлением в пространстве и точкой приложения.
Точку приложения силы можно перенести вдоль ее направления, не изменяя в целом действия силы на тело Но такой перенос точек приложения силы изменяет распределение деформаций и сил упругости в реальном теле.
4 Второй закон Ньютона устанавливает связь между взаимодействием тел и изменением их поступательного движения, и потому он является основным законом динамики поступательного движения.
Если на одно и то же тело действуют разные силы, то оказывается, что ускорение, которое приобретает тело, всегда прямо пропорционально величине приложенной силы:
.
При действии одной и той же силы на тела с разными массами их ускорение будет обратно пропорциональным массе тел:
.
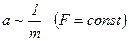Используя эти выражения и учитывая, что сила и ускорение векторные величины, получим:
,
где k – коэффициент пропорциональности, который зависит от выбора единиц измерения. Полученное выражение выражает содержание второго закона Ньютона:
ускорение, приобретаемое телом, прямо пропорционально силе, действующей на него, и обратно пропорционально массе этого тела; по направлению ускорение совпадает с силой:
В системе единиц СИ коэффициент пропорциональности k=1 і
,
5 Если масса – постоянная величина, то
.
Векторная величина 
называется импульсом (количеством движения) материальной точки. Тогда
.
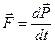Это выражение называется уравнением движения материальной точки и позволяет дать второму закону Ньютона более общую формулировку:
скорость изменение имп. материальной точки равна силе, действующей на точку.
Второй закон Ньютона справедлив лишь в инерциальных системах отсчета.
6При действии на материальную точку нескольких сил выполняется принцип независимости действия сил: если на материальную точку действуют одновременно несколько сил, то каждая из этих сил придает материальной точке ускорение, которое определяется вторым законом Ньютона так, будто других сил не было.
7 Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона:
силы взаимодействия двух материальных точек в инерциальной системе отсчета одинаковы по модулю, направлены в противоположные стороны и действуют вдоль прямой, соединяющей эти точки:
,
где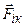 
– сила, действующая на i-ю точку со стороны k-й точки, а 
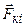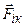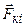– сила, действующая на k-ю точку со стороны i-й. Силы и приложены к разным точкам (рис. 5).
8 Совокупность материальных точек (тел), которые рассматриваются как единое целое, называется механической системой. Силы взаимодействия между материальными точками механической системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система, в которой тела взаимодействуют между собой, и на которую не действуют внешние силы, называется замкнутой.
Рассмотрим механическую систему, которая состоит из n тел, массы и скорости которых равны соответственно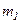 
, 
, ..., 
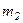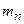и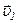 
, 
, ..., 
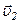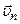. Пусть 
, 
, ..., 
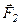– равнодействующие внешних сил, действующих на каждое из этих тел, а 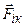– внутренняя сила, действующая на і-е тело со стороны к-го.
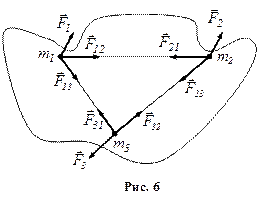
На рис. 6 приведены равнодействующие внешних сил и внутренние силы, которые действуют между телами механической системы, состоящей, например, из трех тел. Запишем второй закон Ньютона для каждого из n тел механической системы:
,
,
.
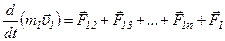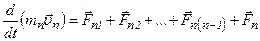Складывая почленно эти уравнения, находим:
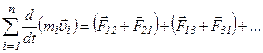
По третьему закону Ньютона
.
Поэтому
и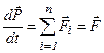 
,
где 
– импульс системы, а 
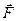– главный вектор внешних сил.
Итак, производная по времени от импульса механической системы равна главному вектору внешних сил, действующих на систему.
В случае замкнутой системы
,
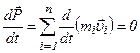то есть
.
Это выражение является законом сохранения импульса: импульс замкнутой системы сохраняется, то есть не изменяется с течением времени.
Контрольные вопросы.
1. Какая система отсчета называется инерциальной? В чем заключается значение первого закона Ньютона?
2. Будет ли система отсчета, связанная с Землей, инерциальной?
3. Какое явление называют инерцией? Приведите примеры проявления инерции.
4. В чем заключается свойство инертности? Как и для чего вводится понятие массы?
5. Какое физическое содержание имеет сила?
6. В чем заключается фундаментальность второго закона Ньютона?
7. В чем заключается принцип независимости действия сил? Как определить результирующую силу?
8. Если ускорение тела равно нулю, означает ли это, что на тело не действуют силы?
9. Сформулируйте третий закон Ньютона. Уравновешиваются ли силы, действующие на тела, упоминаемые
в нем?
10. Какая система называется замкнутой?
11. Сформулируйте и докажите закон сохранения импульса для замкнутой системы тел.
Содержательный модуль 1.1 Кинематика и динамика поступательного и вращательного движений твердого тела
Тема 1.1.3: Работа. Энергия. Закон сохранения энергии. Диссипативные системы.(Самостоятельное изучение)
План.
1 Работа силы;
2 Кинетическая энергия;
3 Потенциальная энергия;
4 Закон сохранения механической энергии;
5 Диссипативные системы. Закон сохранения и превращения энергии.
Литература:
[1] Чолпан П.П. Фізика: Підручник. – К.: Вища шк., 2004. – 567 с.
(стор.71, 55,59,60)
1 Работа А равна скалярному произведению силы 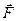на перемещение Δ 
:
A=(F,Δ )=FS 
cosα
Если сила изменяется, то, рассматривая элементарное перемещение d , силу 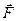можно считать постоянной, а движение точки ее приложения – прямолинейным. Элементарной работой δA по перемещению d называется скалярная величина
- δA=(F,d )=FcosαdS
где dS=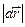 
– элементарный путь.
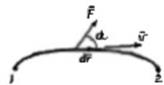
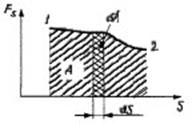
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ:
- A= 
cosα
Если зависимость силы от пути представлена графически, то работа измеряется площадью, заштрихованной на рисунке:
Сила, действующая на тело, не выполняет работу, если:
А) тело пребывает в покое
Б) сила перпендикулярна к направлению перемещения тела
Если на тело, которое движется поступательно, одновременно действуют несколько сил, то работа равнодействующей силы равна алгебраической сумме работ составляющих сил.
Сила называется консервативной или потенциальной, если работа А, которая выполняется этой силой при перемещении из положения 1 в положение 2, не зависит от того по какой траектории произошло это перемещение:
Примерами консервативных сил является сила тяжести, гравитационные силы, силы упругости, силы электростатического взаимодействия между заряженными телами.
2 Кинетической энергией механической системы называется энергия движения этой системы.
Сила F, действующая на тело в состоянии покоя и вызывающая его движение, выполняет работу. При этом энергия подвижного тела возрастает на величину выполненной работы: dЕк=δА
Запишем 2-ой закон Ньютона в скалярной форме; умножив обе части на элементарный путь dS:
m 
dS = FdS
Поскольку v = 
, то
δА = FdS = mvdv = dEк і
Ек = 
Кинетическая энергия зависит от величины массы и скорости движения тела.
Величина кинетической энергии системы зависит от выбора системы отсчета, то есть является величиной относительной.
Потенциальной энергией механической системы называют энергию, зависящую от взаимного расположения всех материальных точек системы и характера консервативных сил, действующих между точками.
Работа А12, выполняемая консервативными силами при изменении расположения точек системы, определяется начальной и конечной конфигурацией системы. То есть работу А12 можно представить в виде разности значений некоторой функции, называемой потенциальной энергией.
А12=Еп1-Еп2=-(Еп2-Еп1)
Соответственно элементарная работа dА консервативных сил при малом изменении конфигурации системы:
dА=-dЕп или (F,dґ) =-dЕп
Проинтегрировав, получаем:
Еп = -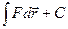 
С – постоянная интегрирования.
1) потенциальная энергия материальной точки в поле тяжести Земли. Определяется по формуле:
Еп = mgh, где h – высота тела над поверхностью Земли
Около поверхности Земли Еп=0.
2) Потенциальная энергия материальной точки в поле центральных сил.
Центральными называются силы, если они направлены вдоль прямых, проходящих через одну и ту же неподвижную точку – центр сил и зависят лишь от расстояния ґ до центра сил.
Eп = 
Считается, что Еп ( 
) = 0
3) Потенциальная энергия упруго деформированного тела.
Во время деформации упругого тела в нем возникают внутренние силы, препятствующие деформации тела и называемые силами упругости F = kx где k – коэффициент упругости.
Потенциальная энергия Еп =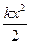 
4 Рассмотрим, как изменяются кинетическая и потенциальная энергия какой-либо изолированной системы, в которой действуют лишь консервативные силы.
Элементарная работа dА консервативных сил равна взятому с противоположным знаком элементарному изменению потенциальной энергии –dEп или изменению кинетической энергии dEк:
dА = dЕк и dA = -dEп
Значит dА=dЕк= - dЕп Или d(Ек+Еп)=0
Откуда: Ек+Еп=сопst
Это равенство является выражением закона сохранения механической энергии, который утверждает, что полная механическая энергия консервативной системы не изменяется.
5Существует еще один вид систем диссипативные системы, в которых механическая энергия постепенно уменьшается за счет превращения в другие формы энергии. Процесс этот называют диссипацией энергии.
При “исчезновении” механической энергии всегда возникает эквивалентное количество энергии другого вида. В этом физическая суть закона сохранения и превращения энергии.
Энергия никогда не исчезает и не появляется снова, она лишь превращается из одного вида в другой.
Контрольные вопросы.
1. В сем заключается отличие между понятиями энергии и работы?
2. Дайте определение консервативной силы.
3. Чему равна работа консервативной силы вдоль замкнутой траектории?
4. Дайте определение кинетической и потенциальной энергии.
5. Сформулируйте закон сохранения механической энергии.
6. Что называется энергией диссипации.
Содержательный модуль 1.1 Кинематика и динамика поступательного и вращательного движений твердого тела
Дата добавления: 2015-10-13; просмотров: 863;