Штучне моделювання нейрона
Біологічний нейрон моделюється як пристрій, що має кілька входів (дендрити) і один вихід (аксон). Кожному входу ставиться у відповідність деякий ваговий коефіцієнт (w), що характеризує пропускну здатність каналу й оцінює ступінь впливу сигналу із цього входу на сигнал на виході. Залежно від конкретної реалізації, оброблювані нейроном сигнали можуть бути аналоговими або цифровими (1 або 0). У тілі нейрона відбувається зважене підсумовування вхідних збуджень, а далі це значення є арґументом активаційної функції нейрона. На рис. 6.2 показана його структура.
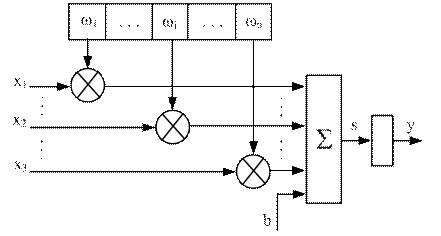
Рисунок 6.2 - Структура штучного нейрона
До складу нейрона входять множники (синапси), суматор і нелінійний перетворювач. Синапси здійснюють зв'язок між нейронами й множать вхідний сигнал на число, що характеризує силу зв'язку – вагу синапса. Суматор виконує додавання сигналів, що надходять по синаптичних зв'язках від інших нейронів, і зовнішніх вхідних сигналів. Нелінійний перетворювач реалізує нелінійну функцію виходу суматора. Ця функція називається функцією активації або передавальною функцією нейрона. Нейрон у цілому реалізує скалярну функцію векторного арґументу. Математична модель нейрона описується наступними співвідношеннями:
 ; (6.1)
; (6.1)
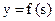 , (6.2)
, (6.2)
де  - вага синапса (
- вага синапса ( 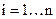 ); b - значення зсуву; s - результат підсумовування;
); b - значення зсуву; s - результат підсумовування;  - компонент вхідного вектора (вхідний сигнал) (
- компонент вхідного вектора (вхідний сигнал) ( 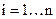 ); y - вихідний сигнал нейрона; n - кількість входів нейрона; f - нелінійне перетворення (функція активації).
); y - вихідний сигнал нейрона; n - кількість входів нейрона; f - нелінійне перетворення (функція активації).
У загальному випадку вхідний сигнал, вагові коефіцієнти й значення зсуву можуть набувати дійсних значень. Вихід y визначається видом функції активації й може бути як дійсним, так і цілим. У багатьох практичних задачах входи, ваги й зсуви можуть набувати лише деяких фіксованих значень.
Синаптичні зв'язки з позитивними вагами називають збуджуючими, з негативними вагами - гальмуючими.
Таким чином, нейрон повністю описується своїми вагами  та передавальною функцією f(s). Одержавши набір чисел (вектор)
та передавальною функцією f(s). Одержавши набір чисел (вектор)  , які є входами, нейрон видає деяке число у на виході.
, які є входами, нейрон видає деяке число у на виході.
На вхідний сигнал s нелінійний перетворювач відповідає вихідним сигналом f(s), що являє собою вихід нейрона y. Приклади активаційних функцій подані в табл. 6.1 і на рис. 6.3.
Таблиця 6.1 - Перелік функцій активації нейронів
| Функція активації | Формула | Область визначення |
| Порогова | 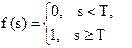
| 
|
| Знакова (сигнатурна) | 
| 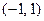
|
| Сигмоїдальна (логістична) | 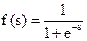
| 
|
| Напівлінійна | 
| 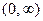
|
| Лінійна | 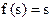
| 
|
| Радіальна базисна (гауссова) | 
| 
|
| Напівлінійна з насиченням | 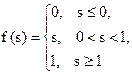
| 
|
| Лінійна з насиченням | 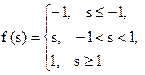
| 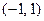
|
| Гіперболічний танґенс (сигмоїдальна) | 
| 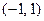
|
| Трикутна | 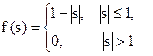
| 
|

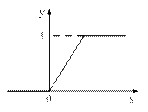


а) б) в) г)
Рисунок 6.3 - Приклади активаційних функцій:
а) - порогова; б) - напівлінійна з насиченням; в) - сигмоїд (логістична функція);
г) - сигмоїд (гіперболічний танґенс)
Дата добавления: 2015-10-13; просмотров: 1112;
