I. Теоретическое введение. Для зарядки различных по форме проводников до одинакового потенциала φ им необходимо сообщить различные по величине заряды
Для зарядки различных по форме проводников до одинакового потенциала φ им необходимо сообщить различные по величине заряды. Это свойство проводников характеризуется величиной, называемой электроемкостью
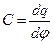(1)
Из формулы (1) видно, что электроемкость уединенного проводника численно равна электрическом заряду, который надо сообщить этому проводнику, чтобы потенциал проводника изменить на единицу.
Уединенным называется проводник, который находится в однородной среде вдали от заряженных тел и других проводников.
Емкость зависит от формы поверхности проводника, его линейных размеров, расположения относительно других тел и от диэлектрической проницаемости окружающей среды. Следует заметить, что электроемкость не зависит ни от заряда проводника, ни от его потенциала, что совершенно не противоречит соотношению (1).
Было замечено, что емкость проводника возрастает при приближении к нему других тел. Дело в том, что при сообщении проводнику А заряда q окружающие его проводники заряжаются через влияние, причем ближайшими наводящими заряд q оказываются заряды противоположного знака. Эти заряды несколько ослабляют поле, создаваемое зарядом q. Таким образом, они понижают потенциал проводника А и повышают его электроемкость.
Наибольший практический интерес представляет система, состоящая из двух, близко расположенных друг от друга проводников, заряды которых численно равны, но противоположны по знаку. Особенно важным для практики является случай, когда два разноименных проводника имеют такую форму и так расположены друг относительно друга, что создаваемое ими электростатическое поле полностью (или относительно полностью) сосредоточено в ограниченной части пространства. Такая система двух тел называется конденсатором, а сами проводники - обкладками конденсатора.
Емкость конденсатора:
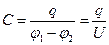(2)
где U = φ1-φ2 - разность потенциалов между обкладками, q - абсолютная величина их зарядов.
.
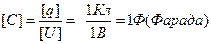Емкость в одну фараду – это ёмкость такого устройства, что, если на него поместить заряд в 1Кл (это колоссальный заряд), то разность потенциалов будет 1В. Нет таких конденсаторов на свете, на Земле просто невозможно
 |
построить такой конденсатор, чтобы он имел ёмкость в 1 фараду, поэтому, подходя к ёмкости, мы будем использовать микрофарады.
Плоский конденсатор состоит из двух параллельных металлических пластин площадью S каждая, расположенных на близком расстоянии d одна от другой (рис.2).
 |
Имеется в виду, что расстояние между пластинами много меньше характерного линейного размера,
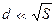, S – площадь пластин. Пластины имеют большую площадь, зазор маленький, в этом случае силовые линии поля однородны и внешние заряды на него не влияют. Из формулы для напряженности одной пластины с поверхностной плотностью заряда 
: 
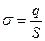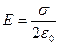, можно определить напряжённость поля между пластинами. Т.к. внутри конденсатора напряженности полей обоих пластин сонаправлены (см.рис.2), то: 
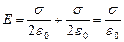. При наличии диэлектрика.
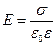(3)
Так как поле однородное, разность потенциалов равняется:
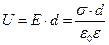(4)
Подставим (4) в (2) и учтем, что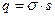 
, будем иметь:
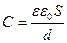(5)
Выражение (5) показывает, что электроемкость конденсатора зависит от площади S его обкладок, расстояния d между ними и диэлектрика с диэлектрической проницаемостью ε. В целях экономии материалов металлические электроды конденсаторов обычно изготавливаются в виде тонкой фольги. В качестве изолирующей прокладки используются парафинированная бумага, полистирол, слюда, керамика, воздух. По типу используемого диэлектрика конденсаторы называются бумажными, слюдяными, полистирольными, керамическими, воздушными.
 |
Бумажный конденсатор изготавливают из двух полос металлической фольги, изолированных друг от друга полосами парафинированной бумаги. Полосы фольги и бумагу сворачивают в рулон и помещают в металлический или фарфоровый корпус (рис.3). Через специальные изоляторы от листов фольги делают два вывода для подключения конденсатора в электрическую цепь.
Аналогичное устройство имеют и конденсаторы других типов.
Все перечисленные типы конденсаторов можно включать в электрическую цепь, не обращая внимания на полярность.
Но есть электролитические конденсаторы, которые необходимо включать, в цепь с учетом полярности. Слоем изолятора в электролитическом конденсаторе служит тонкая пленка оксида алюминия на алюминиевой фольге, помещенной в электролит. Малая толщина пленки алюминия позволяет изготавливать электролитические конденсаторы большой электроемкости при малых размерах обкладок.
Необходимость соблюдения полярности включения электролитических конденсаторов объясняется тем, что пленка оксида алюминия является хорошим изолятором лишь при одном направлении вектора напряженности электрического поля между обкладками конденсатора. Изменение направления вектора напряженности приводит к значительному уменьшению электрического сопротивления изолирующего слоя. Электрический ток, протекающий через конденсатор, вызывает его разогревание. При достаточно большой разности потенциалов происходит разрушение слоя изолятора, наступает пробой конденсатора. Поэтому электролитические конденсаторы нельзя включать в цепь переменного тока.
Наряду с конденсаторами постоянной электроемкости в практике применяются конденсаторы переменной электроемкости. В этих конденсаторах электроемкость регулируется изменением взаимного положения пластин. При увеличении площади пластин, находящихся друг против друга, электроемкость увеличивается, при уменьшении — уменьшается.
Помимо емкости, каждый конденсатор характеризуется рабочим или «пробивным» напряжением UМАХ, которое можно прикладывать к обкладкам, не опасаясь пробоя, то есть электрического разряда через слой диэлектрика в конденсаторе. Можно расширить число возможных значений емкости и рабочего напряжения, соединяя несколько конденсаторов в батареи.
 |
При последовательном соединении конденсаторов (рис.4) полная разность потенциалов распределяется между отдельными конденсаторами, причем потенциал соединенных между собой пластин конденсаторов одинаков, а весь заряд батареи равен заряду каждого конденсатора в отдельности.
Емкость такой батареи определяется по формуле:
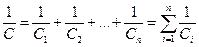(6)
Для получения больших электроемкостей конденсаторы соединяют параллельно (рис.5). Для этого случая емкость батареи равна сумме электроемкостей отдельных конденсаторов
 |
С = С1 + С2 + С3 + ... + Сn или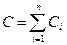 
(7)
Дата добавления: 2015-10-13; просмотров: 1337;