I. Теоретическое введение. Пространство, в котором находится электрический заряд, обладает определенными физическими свойствами
Пространство, в котором находится электрический заряд, обладает определенными физическими свойствами. Так на всякий другой заряд, внесенный в это пространство, действуют электростатические силы Кулона. Если в пространстве действуют какие-либо силы, то говорят, что в нем существует силовое поле.
Для количественного описания электрического поля вводится ряд специальных физических величин. Такой величиной является напряженность электрического поля - силовая характеристика поля.
Напряженностью в любой точке электрического поля называется вектор 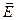 , численно равный силе, с которой это поле действует на единичный положительный заряд, помещенный в данную точку, и направленный в сторону действия силы, то есть:
, численно равный силе, с которой это поле действует на единичный положительный заряд, помещенный в данную точку, и направленный в сторону действия силы, то есть:
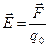 (1)
(1)
Напряженность электрического поля точечного заряда определяется по формуле:
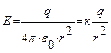 , (2)
, (2)
где 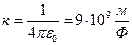 ,
, 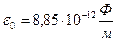 - электрическая постоянная.
- электрическая постоянная.
Если электрическое поле создается не в вакууме, а в веществе, то напряженность поля уменьшается в ε раз. Величина ε называется диэлектрической проницаемостью вещества. Она показывает во сколько раз напряженность электрического поля в вакууме (Е0) больше, чем напряженность электрического поля в среде (Е):
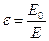 . (3)
. (3)
Если напряженность поля одинакова во всех точках поля, то такое поле называется однородным. Если же величина напряженности поля меняется от точки к точке, то оно называется неоднородным.
Наглядный геометрический образ поля можно получить с помощью так называемых силовых линий.
Силовой линией электрического поля называется такая линия, касательная к которой в каждой ее точке совпадает с вектором напряженности поля в этой точке. Силовым линиям приписывается направление, совпадающее с направлением вектора напряженности 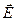 .
.
Свойства силовых линий:
1. Силовые линии являются незамкнутыми линиями.
2. Силовые линии электрического поля начинаются на положительных зарядах и оканчиваются на отрицательных зарядах (либо уходят в бесконечность).
3. Силовые линии не пересекаются.
4. Силовые линии тем гуще, чем больше напряженность электрического поля.
Напряженности электрических полей точечного заряда, диполя, заряженной пластинки и плоскости зависят от свойств среды. Поэтому для характеристики электрического поля целесообразно ввести такую величину, которая не зависела бы от диэлектрической проницаемости среды. Этому условию удовлетворяет величина:
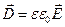 (4)
(4)
Физическая величина D называется электрическим смещением, или индукцией электрического поля.
Рассмотрим сначала однородное электрическое поле у которого во всех точках значение вектора 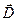 одинаково.
одинаково.
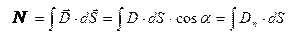 |
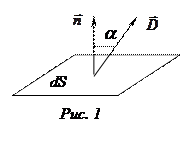
Выделим на плоскости MN участок площадью S. Тогда поток вектора электрического смещения, или просто поток смещения ND (поток электрической индукции) сквозь плоскую поверхность S по определению равен:
(5)
 где Dn – проекция вектора
где Dn – проекция вектора 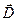 на направление нормали к плоской поверхности dS (рис.1)
на направление нормали к плоской поверхности dS (рис.1)
Для потока вектора электрического смещения выполняется теорема Остроградского-Гаусса:
Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охватываемых этой поверхностью
ND = Sqi (6)
На свободный заряд q, находящийся в электрическом поле, действует сила F = qЕ, приводящая его в движение. Работа dА, совершаемая силой F, при перемещении заряда q на отрезок dl равна
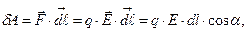 (7)
(7)
где α - угол между направлениями векторов 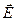 и
и 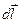 .
.
В случае конечного перемещения заряда из точки "1" в точку "2" работа сил поля равна:
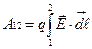 (8)
(8)
Пусть поле создано точечным зарядом q>О Тогда dl cosα = dr напряженность поля точечного заряда 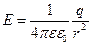 и работа совершаемая при перемещении заряда q0, будет равна:
и работа совершаемая при перемещении заряда q0, будет равна:
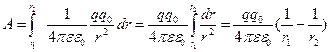 (9)
(9)
то есть работа, совершаемая при перемещении заряда qo в поле точечного заряда q, не зависит от формулы пути, а только от конечного и начального положений заряда q0.
Если заряд перемещается вдоль замкнутого контура L, т.е. его конечное положение совпадает с начальным, то перемещение заряда будет равно нулю, а значит и работа по перемещению заряда по замкнутому контуру равна нулю.
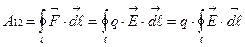 =0.
=0.
Тогда следует, что 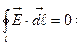 .
.
Данный интеграл называется циркуляцией вектора напряженности электрического поля вдоль замкнутого контура.
 | |||||
 |  | ||||
Силовое поле, напряженность которого удовлетворяет условию
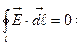 называется потенциальным. Поэтому работа А равна убыли потенциальной энергии
называется потенциальным. Поэтому работа А равна убыли потенциальной энергии  W этого заряда, взятой с обратным знаком:
W этого заряда, взятой с обратным знаком:
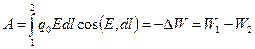 (10)
(10)
Отношение 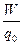 обозначается φ и называется потенциалом данной точки электростатического поля.
обозначается φ и называется потенциалом данной точки электростатического поля.
Тогда, потенциал точки поля, созданным точечным положительным зарядом q, на расстоянии r равен:
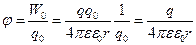 (11)
(11)
 Работу, совершаемую силами электростатического поля, по перемещению заряда q0 из точки А в точку В можно записать как
Работу, совершаемую силами электростатического поля, по перемещению заряда q0 из точки А в точку В можно записать как
A = WA – WB = q0 φА - q0 φВ = q0 (φА – φВ) (12)
 где φА – φВ - соответственно потенциалы точек А и В.
где φА – φВ - соответственно потенциалы точек А и В.
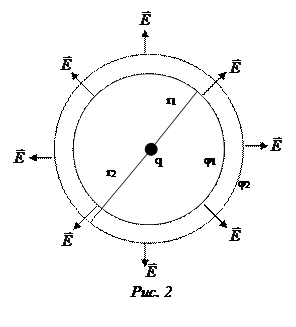 Геометрическое место точек с одинаковым потенциалом называется эквипотенциальной поверхностью. Так как, потенциал постоянен лишь вдоль кривых, перпендикулярных к силовым линиям поля, то и эквипотенциальные поверхности должны быть везде перпендикулярными к силовым линиям.
Геометрическое место точек с одинаковым потенциалом называется эквипотенциальной поверхностью. Так как, потенциал постоянен лишь вдоль кривых, перпендикулярных к силовым линиям поля, то и эквипотенциальные поверхности должны быть везде перпендикулярными к силовым линиям.
Электростатическое поле можно изобразить графически не только при помощи силовых линий, но и при помощи эквипотенциальных поверхностей (рис.2). Вокруг каждой системы зарядов можно провести бесконечное множество эквипотенциальных поверхностей.
Определим, как связаны между собой напряженность и потенциал электростатического поля. Рассмотрим перемещение заряда qo с одной эквипотенциальной поверхности на другую.
Из формул (7) и (12) следует, что
dА = - qo · dφ
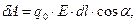
где dl×cosα = dr следовательно
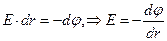 , (13)
, (13)
где dφ – разность потенциалов между двумя близлежащими точками, dr – расстояние между этими точками.
Знак «-» показывает, что вектор напряженности электростатического поля направлен в сторону убывания потенциала.
Дата добавления: 2015-10-13; просмотров: 1265;
