Показатели вариации и способы их расчета

Показатели вариации делятся на две группы: абсолютные и относительные.

К абсолютным показателям относятся:

─ размах вариации,

─ среднее линейное отклонение,

─ дисперсия

─ среднее квадратическое отклонение.

К относительным показателям вариации относятся:

─ коэффициент вариации,

─ относительное линейное отклонение и др.

Размах вариации (R) вычисляется как разность между наибольшим и наименьшим значениями варьирующего признака

.

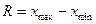Он показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое (х_min) и самое большое значение признака (х_max).

Например, различие между максимальной и минимальной пенсией отдельных групп населения, уровнем дохода различных категорий работающих или нормами выработки у рабочих определенной специальности или квалификации.

Размах является важной характеристикой вариации, он дает первое общее представление о различии единиц внутри совокупности. Размах вариации выражается в тех именованных числах, в каких выражены значения признака.

Особенность показателя размаха вариации заключается в том, что он зависит лишь от двух крайних значений признака. По этой причине его целесообразно применять в тех случаях, когда особое значение имеет либо минимальный, либо максимальный вариант, т. е. когда размах вариации имеет важное смысловое значение.

Например, им определяются пределы, в которых могут колебаться размеры тех или иных параметров деталей; его используют при испытании стальных тросов на разрыв и т. п.

Другая сторона этой особенности заключается в том, что на величину размаха вариации большое влияние оказывает случайность. Так как из статистического ряда берутся только два значения признака, причем крайние в ряду, на размах этих значений могут оказывать влияние причины случайного характера, то и размах вариации может быть зависимым от случайных причин.

С отмеченной особенностью связано и то обстоятельство, что показатель размаха вариации не учитывает частот в вариационном ряду распределения.

Среднее линейное отклонение. Показатель размаха вариации дает обобщающую характеристику только границам (амплитуде) значений признака, но не дает характеристики вариации распределению отклонений. Распределение отклонений можно уловить, вычислив отклонения всех вариант от средней. А для того, чтобы дать им обобщающую характеристику, необходимо далее вычислить среднюю из этих отклонений, т. е. разности между значением признака и средней арифметической в данной совокупности единиц.

Из свойства средней арифметической (свойство 2) нам известно, что сумма отклонений значений признака от нее всегда равна нулю, так как сумма положительных отклонений всегда равна сумме отрицательных отклонений. Следовательно, чтобы вычислить среднюю арифметическую из отклонений, нужно условно допустить, что все отклонения, положительные и отрицательные, имеют одинаковый знак. Тогда, если взять сумму всех отклонений, условно принятых с одинаковым знаком, и разделить на их число, то полученный показатель вариации будет называться средним линейным отклонением ( 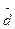), т. е. это средняя арифметическая из абсолютных значений отклонений отдельных вариантов от их средней арифметической.

Если каждый вариант в ряду распределения повторяется один раз, то среднее линейное отклонение равно

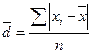
где 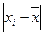— абсолютные значения отклонений отдельных вариантов от их средней величины;

n — объем совокупности.

Для вариационного ряда с неравными частотами формула имеет следующий вид:

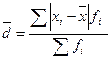, (6.1)

где 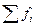— сумма частот вариационного ряда.

Пример.

На основе данных дискретного ряда распределения табл. 6.1. рассчитаем размах вариации и среднее линейное отклонение:

Таблица 6.1

Группы сотрудников по стажу работы, лет (х)	Число сотрудников, в % к итогу (f)
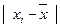
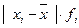
А
			-2
			-1
Итого:				X

Решение.

1) Размах вариации стажа работы равен

R= 12- 8 = 4 (года).

2) Определим среднее линейное отклонение по формуле 6.1.
Результаты вспомогательных расчетов даны в табл. 6.1 графы 3-5.

Средний стаж работы сотрудников определяем по формуле средней арифметической взвешенной (графа 2)

.

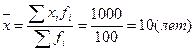Отклонения индивидуальных значений стажа от средней с учетом и без учета знака содержатся в графах 3 и 4, а произведения отклонений по модулю на соответствующие частоты даны в графе 5.

Среднее линейное отклонение стажа работы сотрудников коммерческого банка составит

,

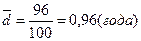т. е. конкретные значения стажа работы сотрудников в среднем отклоняются от среднего значения признака на 0,96 года.

Среднее линейное отклонение обладает большим преимуществом перед размахом вариации в отношении полноты характеристики колеблемости признака. Однако при этом в некотором смысле нарушается элементарное правило математики, так как отклонение от среднего значения признака складывается без учета знаков.

Это обстоятельство вынуждает искать такой показатель вариации, который был бы лишен и этого недостатка. Хотя в некоторых случаях суммирование показателей без учета знаков имеет экономический смысл.

Например, в практической статистике оборот внешней торговли страны определяется как сумма экспорта и импорта, общий оборот рабочей силы — как сумма принятых и уволенных и т. д.

Отмеченный выше недостаток среднего линейного отклонения может быть устранен путем возведения в квадрат отклонений вариантов от средней величины.

Дисперсия представляет собой средний квадрат отклонения значений признака от их средней величины. Порядок ее вычисления можно выразить следующими формулами.

Если каждый вариант повторяется один раз, то дисперсия равна

.

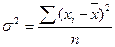Для вариационного ряда с неравными частотами формула примет

вид

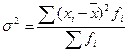(6.2)

Квадратный корень из дисперсии носит название среднего квадра-гического отклонения от средней. Формулы его расчета следующие:

,

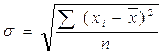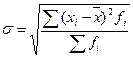. (6.3)

Элементарное алгебраическое преобразование формулы среднего квадратического отклонения приводит ее к следующему виду:

.

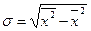Эта формула часто оказывается более удобной в практике расчетов.

Среднее квадратическое отклонение так же, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется такое соотношение

.

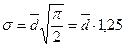Зная это соотношение, можно по известному показателю определить неизвестный, например, по 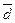определить σ и наоборот. Среднее квадратическое отклонение измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака (рублях, тоннах, процентах и т. д.). Оно является абсолютной мерой вариации.

Пример.

Покажем расчет среднего квадратического отклонения по данным дискретного ряда рао пределения студентов одного из факультетов по возрасту (табл. 6.2).

Таблица 6.2

Группы студентов по возрасту лет (х)	Число студентов (f)		( )
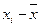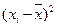
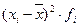
А
			-3.9	15.21	304.2
			-2.9	8.41	672.8
			-1,9	3,61	342,9
			-0,9	0,81	89,1
			0,1	0,01	1,3
			1,1	1,21	205,7
			2,1	4,41	396,9
			3,1	9,61	576,6
Итого			X	X	2571,5

Решение

Результаты вспомогательных расчетов даны в табл. 6.2, графы 2-5.

1) Средний возраст студента определим по формуле средней арифметической взвешенной (графа 2)

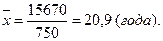
2) Отклонения индивидуального возраста студента от среднего, их квадраты содержатся в графах 3-4, а произведения квадратов отклонений на соответствующие частоты - в графе 5.

Дисперсию и среднее квадратическое отклонение возраста студентов определим по формулам 6.2 и 6.3

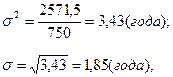
т. е. конкретные значения возраста студентов в среднем отклоняются от их среднего значения на 1,85 года.

Коэффициент вариации. По своему абсолютному значению среднее квадратическое отклонение зависит не только от степени вариации признака, но и от абсолютных уровней вариант и средней. Поэтому сравнивать средние квадратические отклонения вариационных рядов с различными средними уровнями непосредственно нельзя. Чтобы иметь возможность для такого сравнения, нужно найти удельный вес среднего отклонения (линейного или квадратического) в среднем арифметическом показателе, выраженный в процентах, т. е. рассчитать относительные показатели вариации. Формулы коэффициента вариации таковы:

.

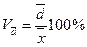Данный показатель в статистике называется линейным коэффициентом вариации.

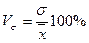(6.4)

Данный показатель называется коэффициентом вариации.

Коэффициент осцилляции (V_R):

.

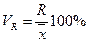В коэффициентах вариации устраняются не только несопоставимость, связанная с различными единицами измерения изучаемого признака, но и несопоставимость, возникающая вследствие различий в величине средних арифметических. Кроме того, показатели вариации дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

Пример.

По данным табл. 6.2 и выполненным выше расчетам определим коэффициент вариации но формуле 6.4

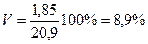
Полученная величина свидетельствует о том, что совокупность студентов по возрасту однородна по своему составу.

Важная функция обобщающих показателей вариации — это оценка надежности средних. Чем меньше 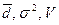, тем однороднее полученная совокупность явлений и надежнее полученная средняя. Согласно «правилу трех сигм» в нормально распределенных или близких к ним рядах отклонения от средней арифметической, не превосходящие ±3σ, встречаются в 997 случаях из 1000. В других рядах распределения эти отклонения встречаются в 89 случаях из 100. Таким образом, зная 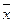и σ, можно получить общее первоначальное представление о вариационном ряде. Если, например, средняя заработная плата рабочего по фирме составила 3600 руб., а равняется 30 руб., то с вероятностью, близкой к достоверности, можно утверждать, что заработная плата рабочих фирмы колеблется в пределах (3600±30), т. е. от 3570 до 3630 руб.